https://paddlepedia.readthedocs.io/

Softmax 回归原理

Softmax回归是逻辑回归 (Logistic Regression) 的推广，逻辑回归适用于二元分类的问题，而Softmax回归适用于多分类的问题。

与线性回归一样，softmax回归也是一个单层神经网络。 由于计算每个输出\(o_1\)、\(o_2\)和\(o_3\)取决于 所有输入\(x_1\)、\(x_2\)、\(x_3\)和\(x_4\)， 所以softmax回归的输出层也是全连接层。

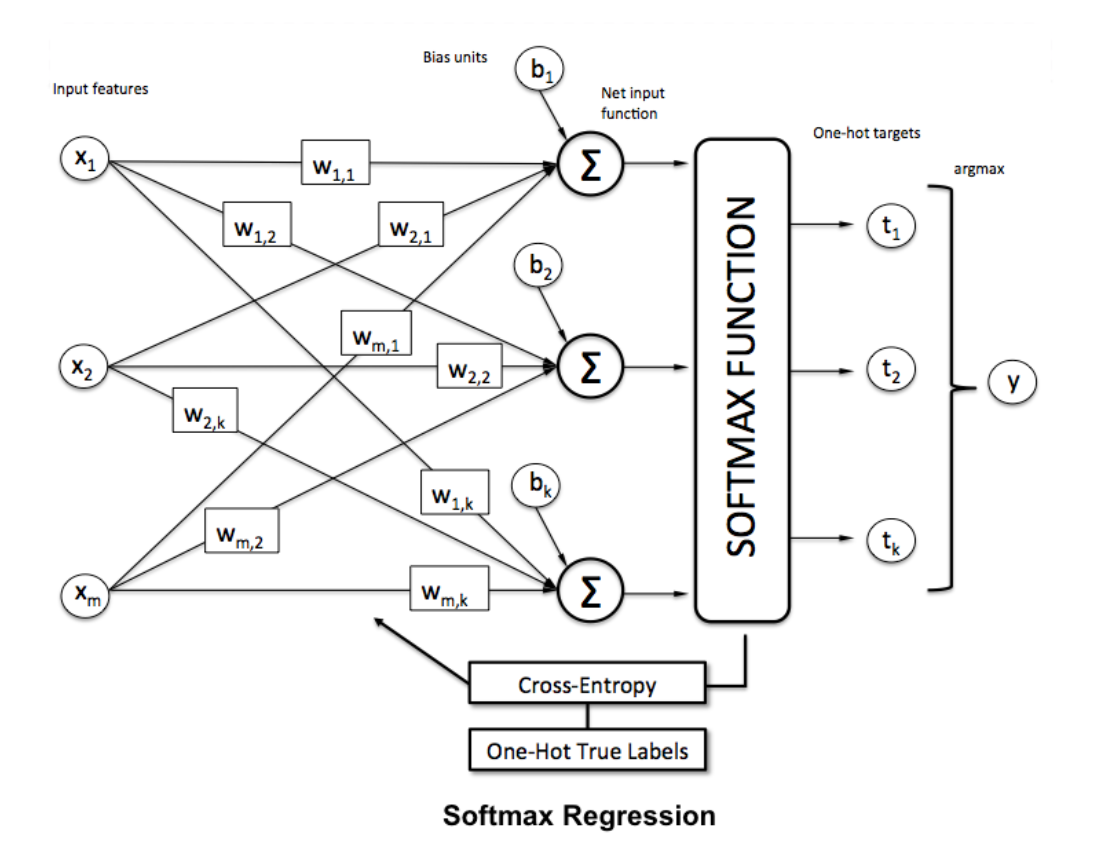
Softmax回归是使用Softmax运算使得最后一层输出的机率分布总和为1，举一个例子，假设我们要辨识手写数字0~9，输入一张数字的影像后，经由Softmax 回归，最后将会输出该影像属于0 ~ 9 个别的机率为何，且其个别的机率总和为1。

\[\hat{\mathbf{y}}=\operatorname{softmax}(\mathbf{o}) \quad \text { 其中 } \quad \hat{y}_{j}=\frac{\exp \left(o_{j}\right)}{\sum_{k} \exp \left(o_{k}\right)}\]

Softmax 函数通常会放在类神经网路的最后一层，将最后一层所有节点的输出都通过指数函数 (exponential function)，并将结果相加作为分母，个别的输出作为分子。

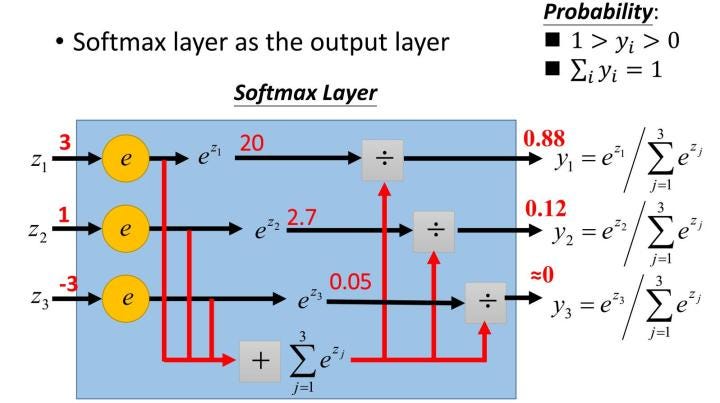
实际计算举例

\[\begin{split}\left[\begin{array}{c} 1.4 \\ -0.1 \\ 0.3 \end{array}\right] \rightarrow \operatorname{softmax} \rightarrow\left[\begin{array}{c} \frac{\mathrm{e}^{1.4}}{\mathrm{e}^{1.4}+\mathrm{e}^{-0.1}+\mathrm{e}^{0.3}} \\ \frac{\mathrm{e}^{-0.1}}{\mathrm{e}^{1.4}+\mathrm{e}^{-0.1}+\mathrm{e}^{0.3}} \\ \frac{\mathrm{e}^{0.3}}{\mathrm{e}^{1.4}+\mathrm{e}^{-0.1}+\mathrm{e}^{0.3}} \end{array}\right]=\left[\begin{array}{l} 0.643 \\ 0.143 \\ 0.214 \end{array}\right]\end{split}\]

什么是One-hot encoding？

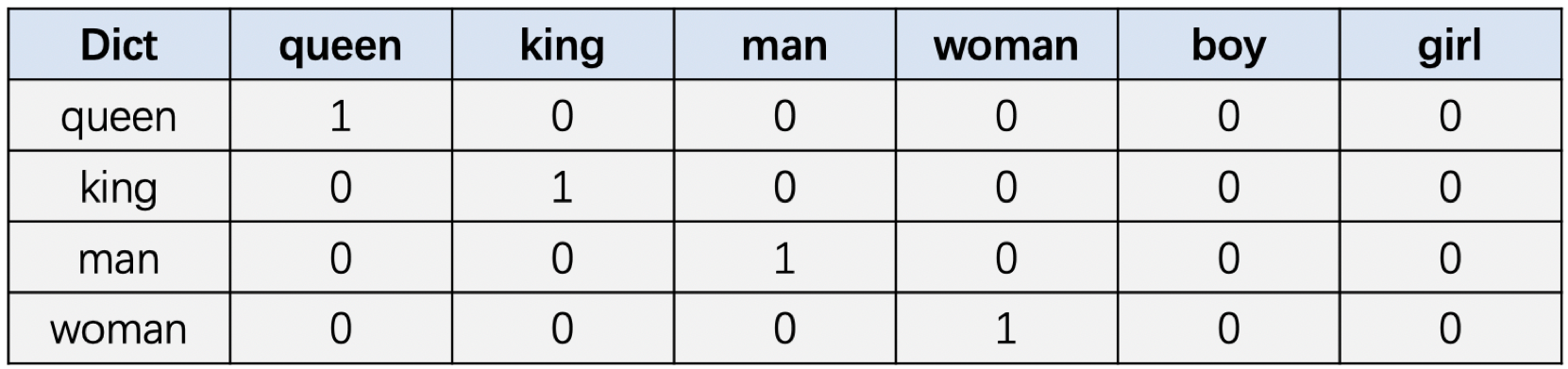
One-Hot编码: 一种简单的单词编码方式。在NLP领域，如何将单词数值化呢，One-Hot编码就是一种很简单的方式。假设我们现在有单词数量为\(N\)的词表，那可以生成一个长度为\(N\) 的向量来表示一个单词，在这个向量中该单词对应的位置数值为1，其余单词对应的位置数值全部为0。举例如下：

词典: [queen, king, man, woman, boy, girl ]

手写辨识实作

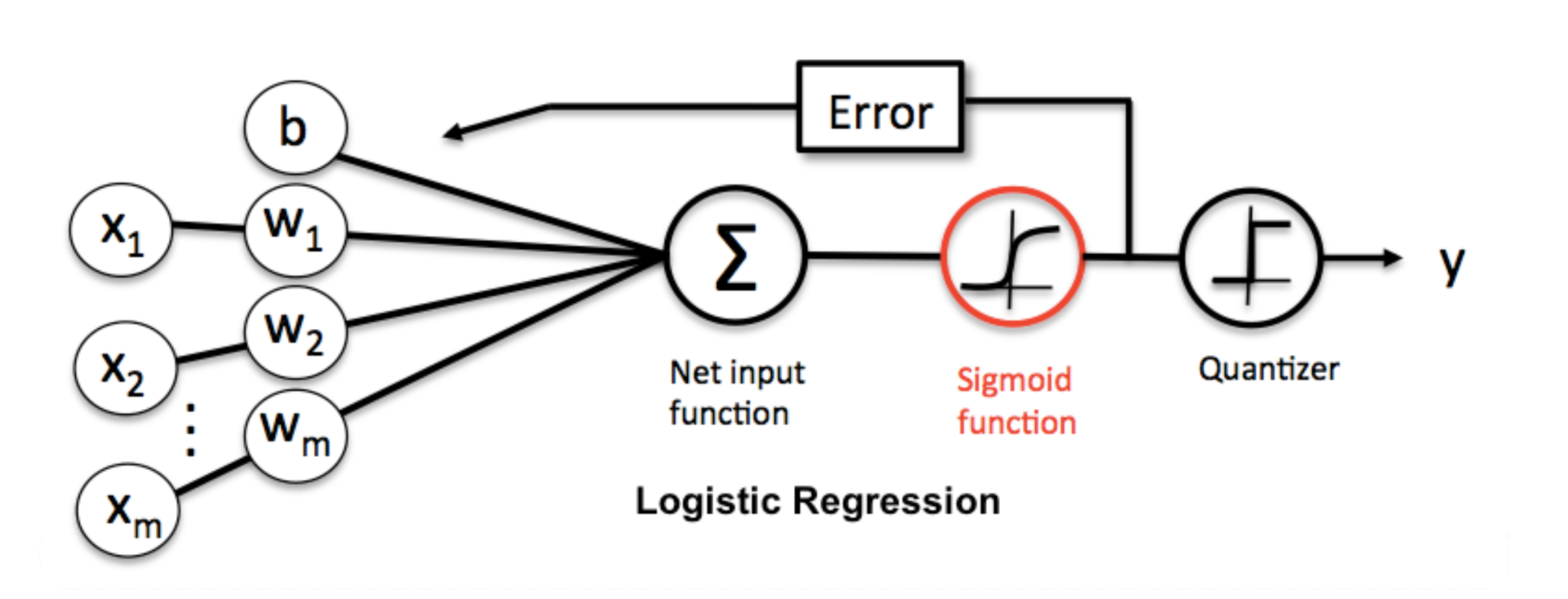
手写辨识是一个非常经典的深度学习入门范例，该范例是输入一张手写数字 0 ~ 9 的影像，并且通过类神经网路预测该影像为 0 ~ 9 哪一个数字。

在Softmax 回归这个例子中，我们使用的是TensorFlow 官方提供的MNIST 资料集，MNIST 资料集中的影像是28 x 28 = 784 的手写数字影像，如果将其中一张影像的像素(pixels) 以矩阵的方式呈现，可以看到那些数值所呈现的形状即是手写数字的形状，所以我们将利用这些数值来预测手写数字。