Attention 注意力机制

Attention 注意力机制#

本文主要涉及Self-attention和Multi-head attention

Self-attention 自注意力机制#

Transformer模型的一个关键特点是使用了称为注意力层的特殊层。这一层会告诉模型，在处理每个单词的表示时，要对你传递给它的句子中某些单词特别关注（并且忽略其他单词）。

输出的向量就是根据query和key计算得到的权重作用于value上的权重和。

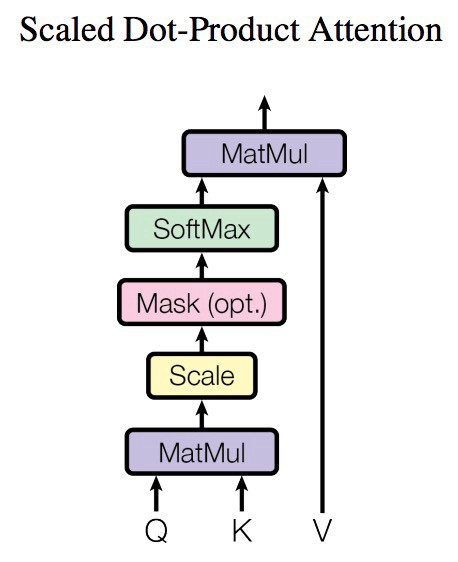
可以看出，自注意力机制的核心过程就是通过Q和K计算得到注意力权重；然后再作用于V得到整个权重和输出。具体的，对于输入Q、K和V来说，其输出向量的计算公式为：

\[\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V\]

公式解读#

  • \(Q\) (Query)：查询矩阵，表示查询某个信息的向量或矩阵。

  • \(K\) (Key)：键矩阵，表示存储的信息的向量或矩阵，用来匹配查询。

  • \(V\) (Value)：值矩阵，表示最终输出的向量或矩阵，通常与键矩阵有对应关系。

  • \(d_k\)：键向量的维度，通常是键和查询的向量维度。

公式中的各部分解释：

  1. 点积\(QK^T\)：

    • 首先，计算查询 \(Q\) 和键 \(K\) 的点积 \(QK^T\)。这个操作用于衡量查询和键的相似性，点积值越高，说明对应的键与查询的相关性越大。

  2. 缩放因子 \(\frac{1}{\sqrt{d_k}}\)：

    • \(d_k\) 是键向量的维度。由于在高维空间中点积值会变得较大，缩放因子 \(\frac{1}{\sqrt{d_k}}\) 用于防止点积值过大导致 softmax 函数输出过于极端，从而使得注意力更加平滑。

  3. softmax：

    • softmax 函数将点积结果转换为概率分布。通过 softmax，可以为每个键计算出与查询的相似性得分。softmax 输出的是归一化的权重，用于衡量各个值的重要性。

  4. 乘以V：

    • 最后，将经过 softmax 计算出的权重与值矩阵 \(V\) 相乘。这个步骤是将注意力权重应用到值上，计算出与查询最相关的信息。每个值的权重是根据与查询的相似性来确定的。

总体流程：

  • 查询 \(Q\) 和键 \(K\) 通过点积和 softmax 计算相似性得分。

  • 根据这个相似性得分，计算不同值 \(V\) 的加权和，输出最终的注意力值。

公式实例（单头）#

我们来通过一个具体的例子，详细解释注意力机制的计算过程。假设我们有以下输入：

  • 查询矩阵\(Q\)、键矩阵\(K\) 和值矩阵\(V\) 分别是\(2 \times 3\) 矩阵，表示有 2 个查询、2 个键和值，向量维度为 3。

  • 假设键向量维度\(d_k = 3\)，取值来自于查询向量\(Q\)和键向量\(K\)的形状。

在多头注意力机制中,参数\(d_{k}\)(每个头的维度)通常是由总的模型维度\(d_{\text{model}}\)和多头注意力的头数\((h)\)决定的。具体来说,\(d_{k}\)通常是这样计算的:

\[d_{k}=\frac{d_{\mathrm{model}}}{h}=\frac{3}{1}\]

Step 1: 给定的矩阵#

假设有以下数据：

\[\begin{split}Q = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix}, \quad K = \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix}, \quad V = \begin{bmatrix} 0 & 2 \\ 1 & 3 \end{bmatrix}\end{split}\]

  • 查询\(Q\) 是一个\(2 \times 3\) 的矩阵。

  • 键\(K\) 也是一个\(2 \times 3\) 的矩阵。

  • 值\(V\) 是一个\(2 \times 2\) 的矩阵。

\(Q,K,V\)的值分别都是通过下图进行运算出来的，我们例子上就不做运算直接举例了

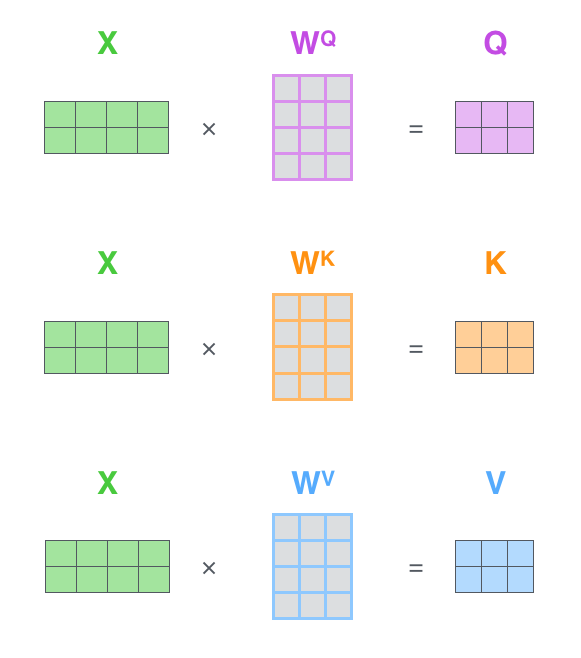
Step 2: 计算点积\(QK^T\)#

点积\(QK^T\)：

\[\begin{split}QK^T = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 2 \end{bmatrix}\end{split}\]

这一步通过查询矩阵\(Q\) 与键矩阵\(K\) 的转置相乘，得到每个查询与所有键的相似性分数。

Step 3: 缩放点积#

为了避免较大的点积值影响 softmax 的效果，我们将点积除以\(\sqrt{d_k}\)，这里\(d_k = 3\)，所以缩放因子为\(\sqrt{3} \approx 1.732\)。因此，缩放后的点积为：

\[\begin{split}\frac{QK^T}{\sqrt{d_k}} = \frac{1}{1.732} \times \begin{bmatrix} 1 & 1 \\ 1 & 2 \end{bmatrix} = \begin{bmatrix} 0.577 & 0.577 \\ 0.577 & 1.154 \end{bmatrix}\end{split}\]

Step 4: 应用 softmax#

接下来，对缩放后的点积应用 softmax 函数。softmax 函数将每一行转化为概率分布。假设第\(i\) 行的点积值为\(a_i\)，那么 softmax 是：

\[\text{softmax}(a_i) = \frac{e^{a_i}}{\sum_j e^{a_j}}\]

对每一行应用 softmax：

  • 对第一行\([0.577, 0.577]\)：

\[\text{softmax}(0.577, 0.577) = \frac{e^{0.577}}{e^{0.577} + e^{0.577}} = \frac{1}{2}, \quad \frac{1}{2}\]

  • 对第二行\([0.577, 1.154]\)：

\[\text{softmax}(0.577, 1.154) = \frac{e^{0.577}}{e^{0.577} + e^{1.154}}, \quad \frac{e^{1.154}}{e^{0.577} + e^{1.154}} \approx 0.40, \quad 0.60\]

softmax 结果为：

\[\begin{split}\text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right) = \begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6 \end{bmatrix}\end{split}\]

Step 5: 加权值矩阵\(V\)#

将 softmax 权重与值矩阵\(V\) 相乘，得到注意力的最终输出：

\[\begin{split}\text{Attention}(Q, K, V) = \begin{bmatrix} 0.5 & 0.5 \\ 0.4 & 0.6 \end{bmatrix} \times \begin{bmatrix} 0 & 2 \\ 1 & 3 \end{bmatrix}\end{split}\]

  • 第一行计算：

\[0.5 \times [0, 2] + 0.5 \times [1, 3] = [0.5, 2.5]\]

  • 第二行计算：

\[0.4 \times [0, 2] + 0.6 \times [1, 3] = [0.6, 2.8]\]

最终的注意力输出为：

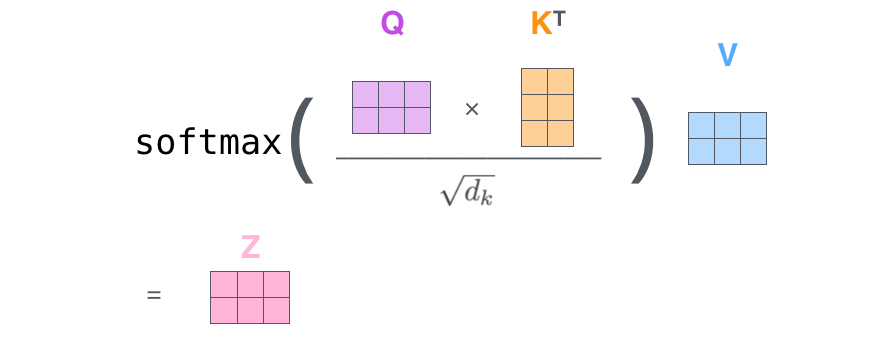
\[\begin{split}\text{Attention}(Q, K, V) = \begin{bmatrix} 0.5 & 2.5 \\ 0.6 & 2.8 \end{bmatrix}\end{split}\]

自注意力机制流程#

假如我们要翻译一个词组”Thinking Machines“，其中Thinking这个词的embedding vector用\(x_1\)表示，Machines这个词的embedding vector用\(x_2\)表示。

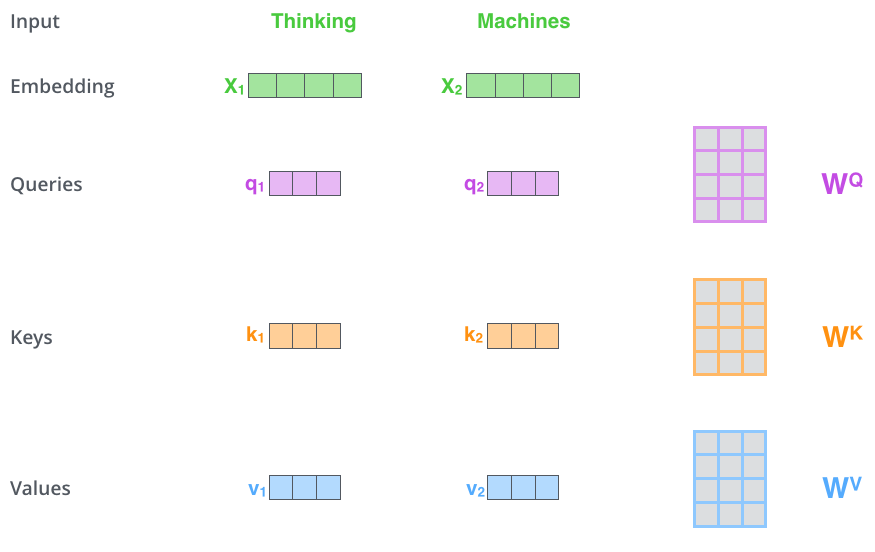
第一步：每个编码器的输入向量（在本例中为每个单词的嵌入）创建三个向量。因此，对于每个单词，我们创建一个查询向量、一个键向量和一个值向量。（将\(x_1\)乘以\(W^Q\)会得到\(q_1\)，我们最终为输入句子中的每个单词创建一个“查询”、一个“键”和一个“值”投影。）

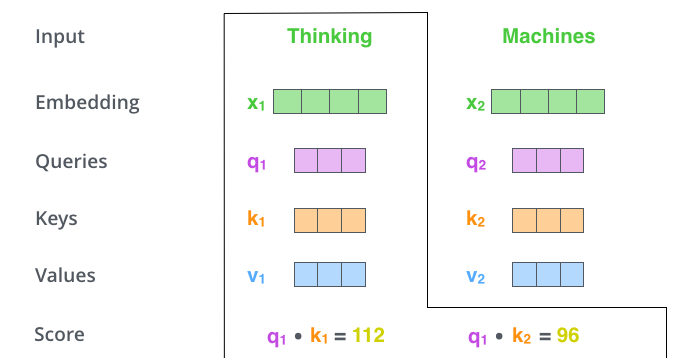
第二步：当我们处理Thinking这个词时，我们需要计算句子中所有词与它的注意力分数（Attention Score），因此，如果我们处理位置\(x_1\)中单词的自注意力，第一个分数将是\(q_1\)和\(k_1\)的点积。第二个分数是\(q_1\)和\(k_2\)的点积。

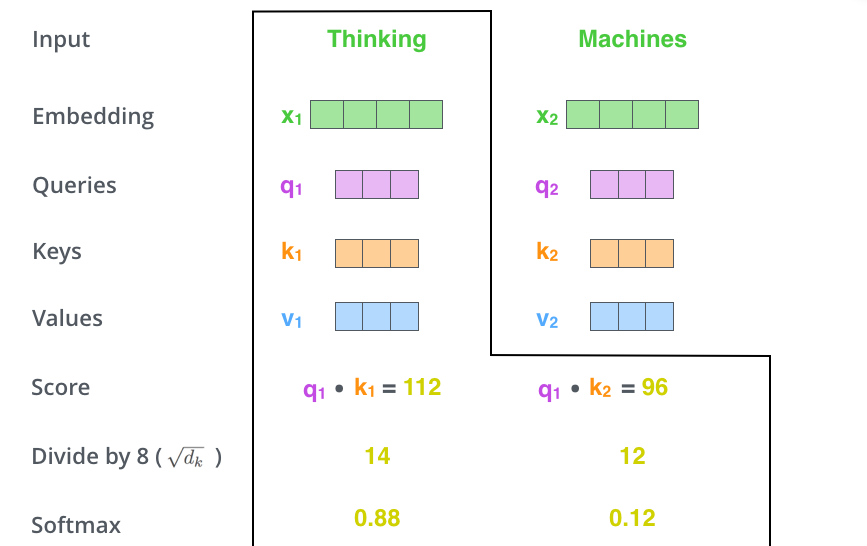
第三步和第四步：分数除以8（论文中使用的关键向量维度的平方根，也就是\(\sqrt{64}\)），然后将结果传递给Softmax运算。Softmax对分数进行归一化，使它们全部为正值并且加起来为1。 第五步：是将每个值向量乘以 softmax 分数（准备将它们相加）。

第六步：对加权值向量求和。这会在该位置（对于第一个单词）产生自注意力层的输出。 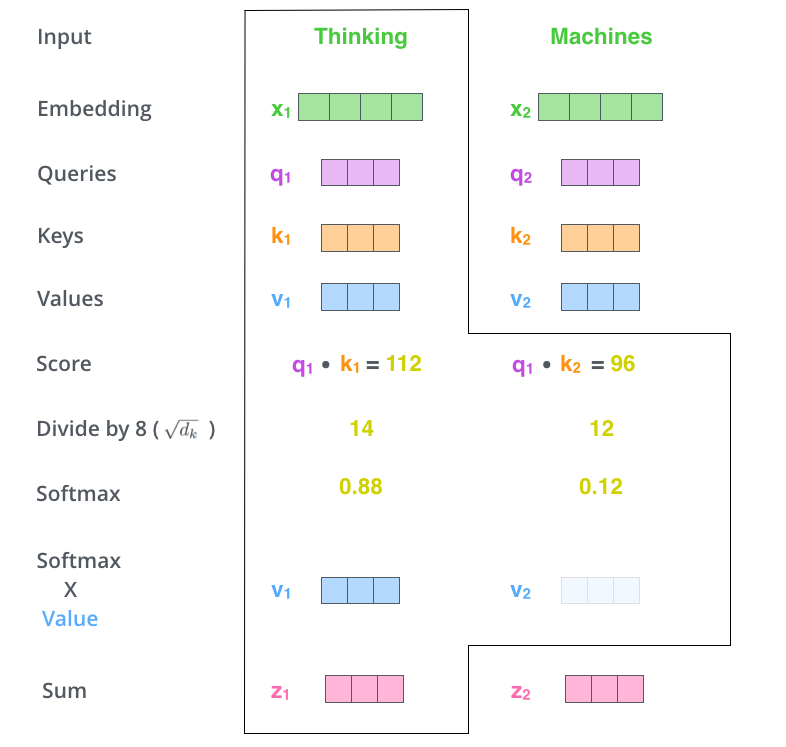自注意力计算到此结束。得到的向量是我们可以发送到前馈神经网络的向量。

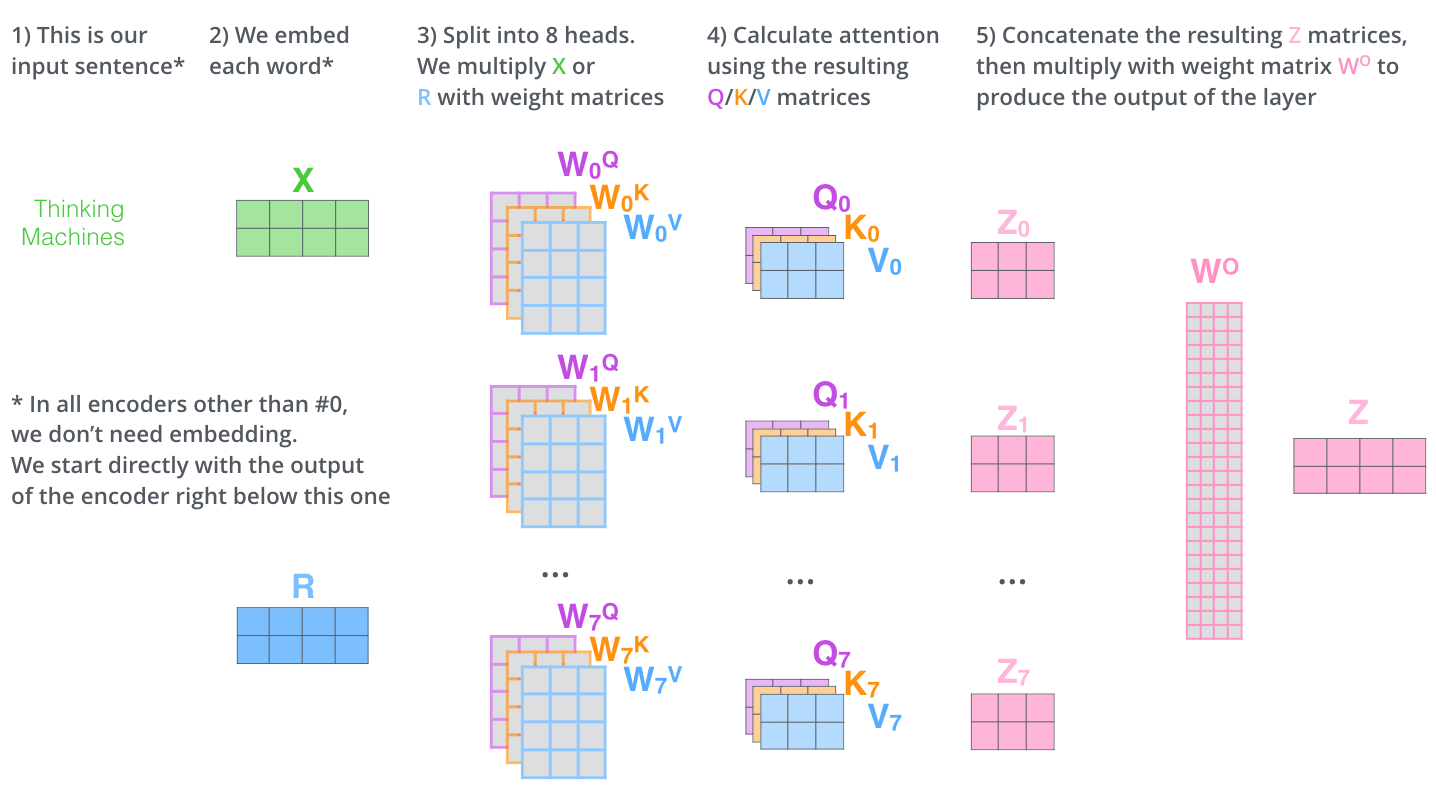
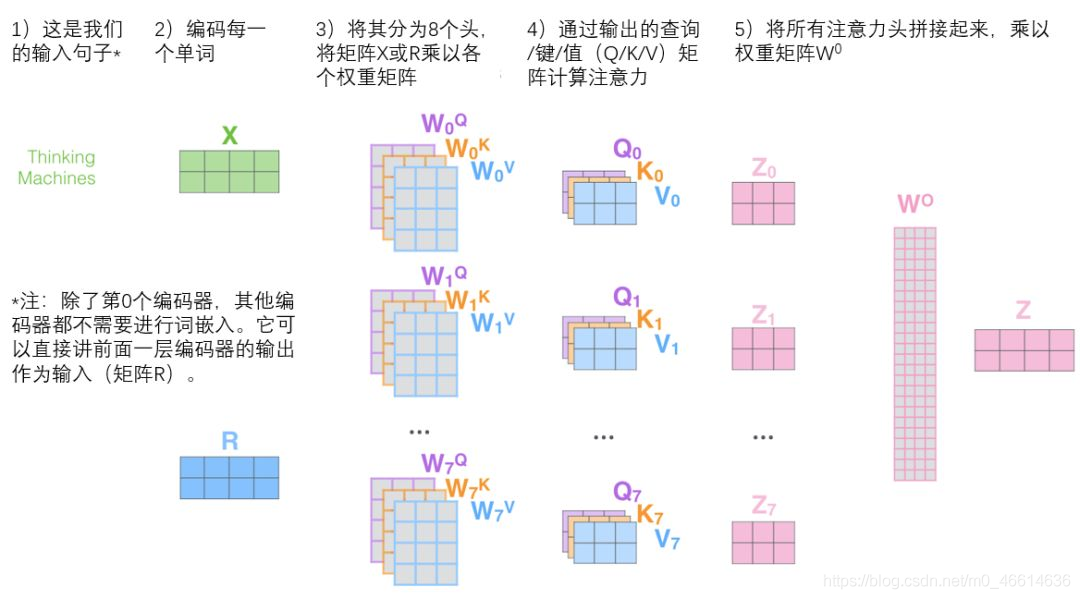
Multi-head attention 多头注意力机制#

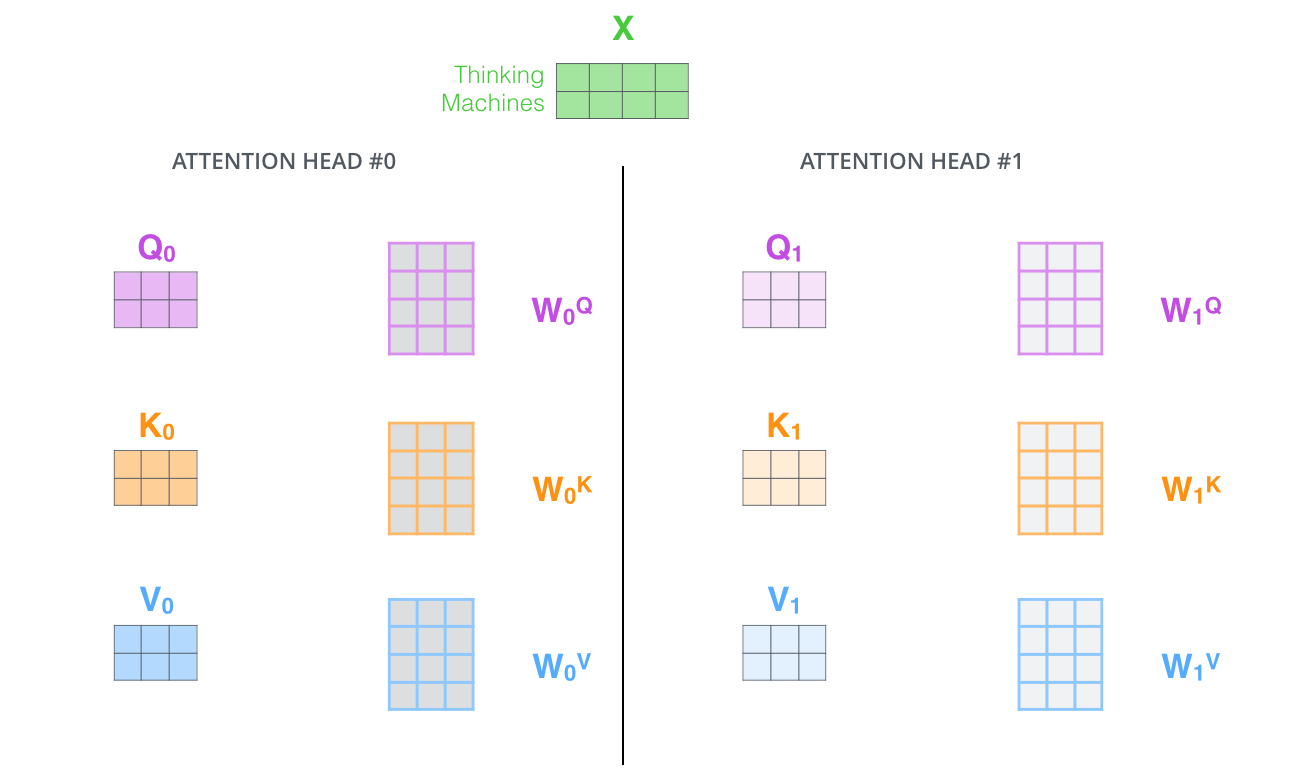
由上面自注意力机制中可以得知，\(Q,K,V\)的矩阵是\(X\)分别乘以\(W^Q,W^K,W^V\)（权重矩阵）得到的。通过多头注意力，我们为每个头维护单独的\(W^Q,W^K,W^V\)（权重矩阵），从而产生不同的\(Q,K,V\)矩阵。

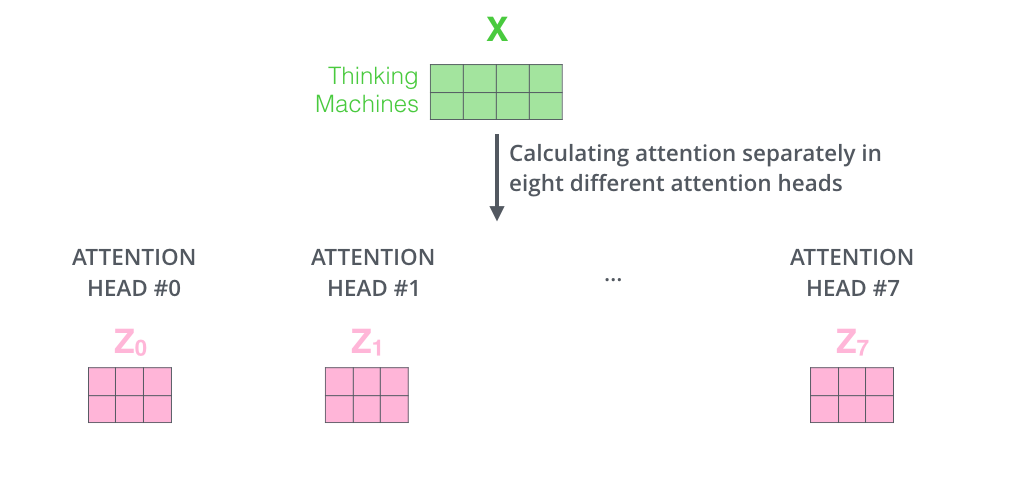
接下来我们会得到8个不同的矩阵\(Z\)

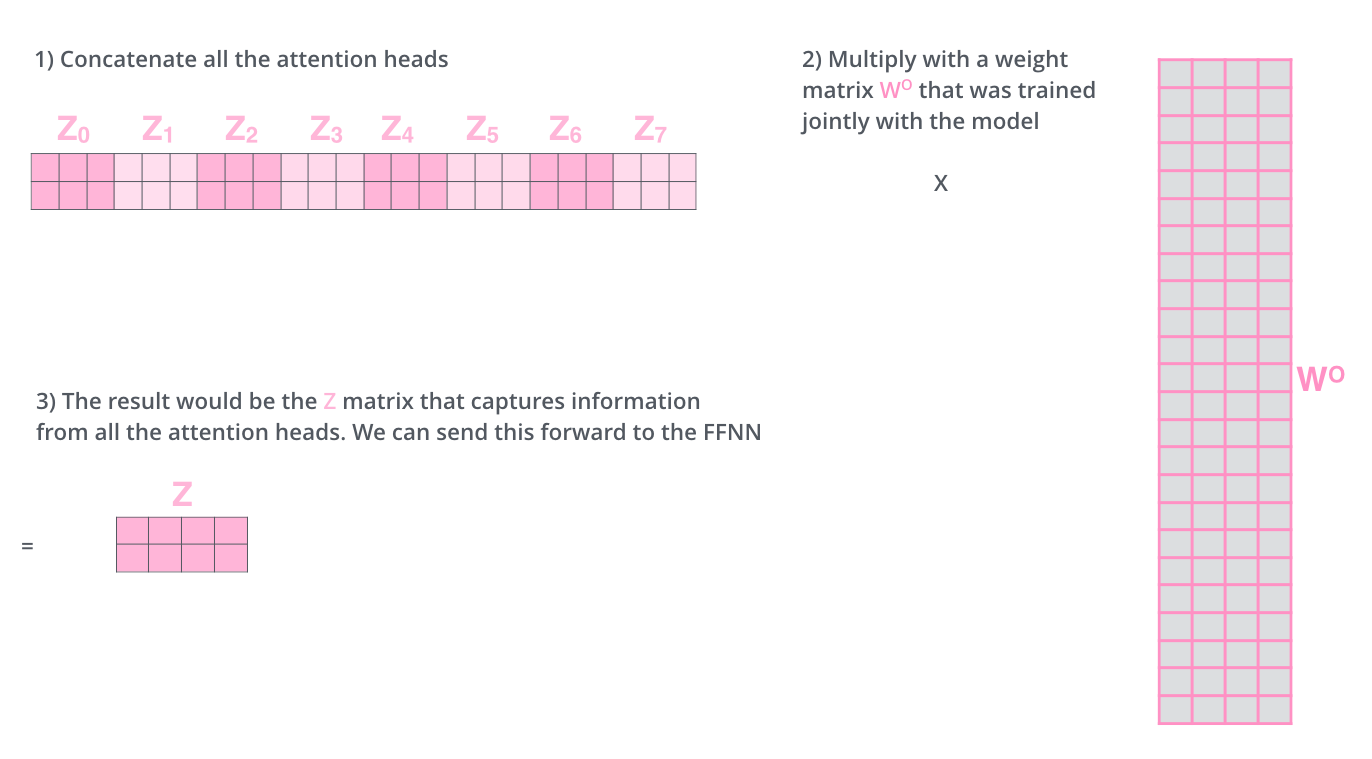
因为最终不需要8个矩阵而是只需要一个，所以需要把这8个不同的矩阵\(Z\)变成一个，如何进行呢？我们将矩阵连接起来，然后将它们乘以一个附加的权重矩阵 \(W^O\)

完整的过程可以参考下面图片

Contents