The Residuals 残差#
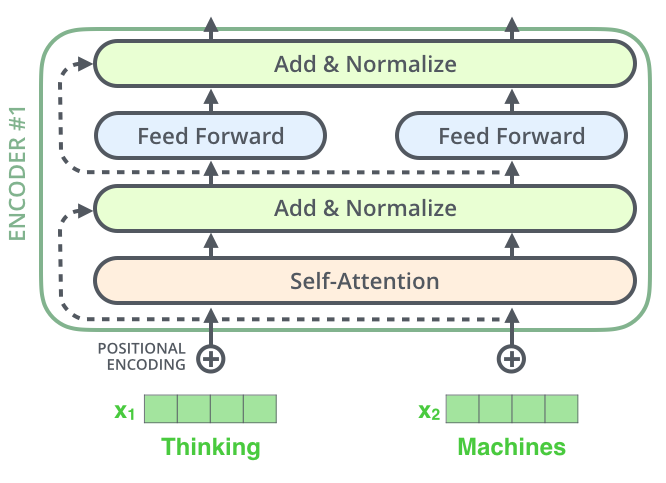
每个编码器中的每个子层(自注意力机制)周围都有一个残差连接,并且后面是层归一化步骤
如果我们要可视化与自注意力相关的向量和层范数操作,它看起来像这样:
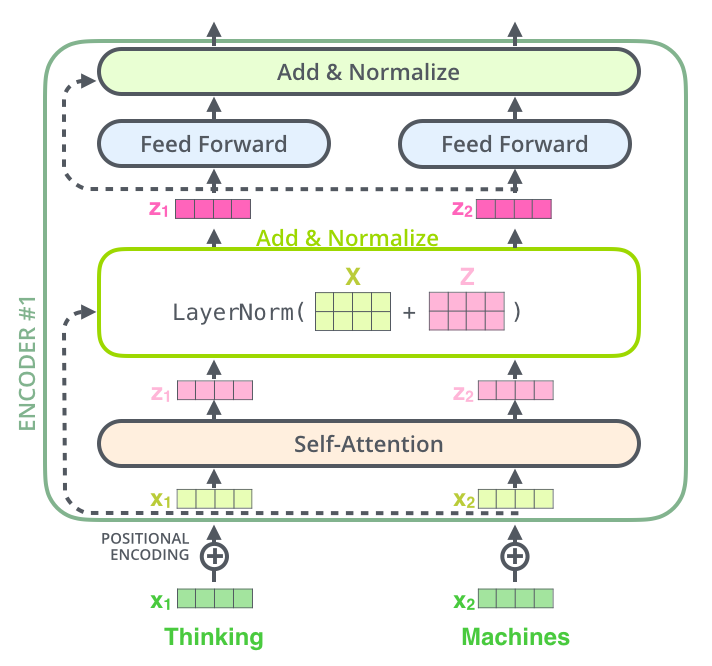
可以看到到上图\(X_1\)到Add & Normalizez,有一条路是经过自注意机制运算的,而另一条路是直接到Add & Normalizez中的,这样做的理由是进过变换可能损失会更大,所以让模型自己选着一条损失小的路线。
残差模块解决了什么问题?#
一定程度上可以缓解梯度弥散问题
现代神经网络一般是通过基于梯度的BP算法来优化,对前馈神经网络而言,一般需要前向传播输入信号,然后反向传播误差并使用梯度方法更新参数。
根据链式法则,当导数<1时,会导致反向传播中梯度逐渐消失,底层的参数不能有效更新,这也就是梯度弥散(或梯度消失);当 导数>1 时,则会使得梯度以指数级速度增大,造成系统不稳定,也就是梯度爆炸问题。此问题可以被标准初始化和中间层正规化方法有效控制,这些方法使得深度神经网络可以收敛。
一定程度上解决网络退化问题
在神经网络可以收敛的前提下,随着网络深度增加,网络的表现先是逐渐增加至饱和,然后迅速下降。
网络退化问题不是过拟合导致的,即便在模型训练过程中,同样的训练轮次下,退化的网络也比稍浅层的网络的训练错误更高,如下图所示。
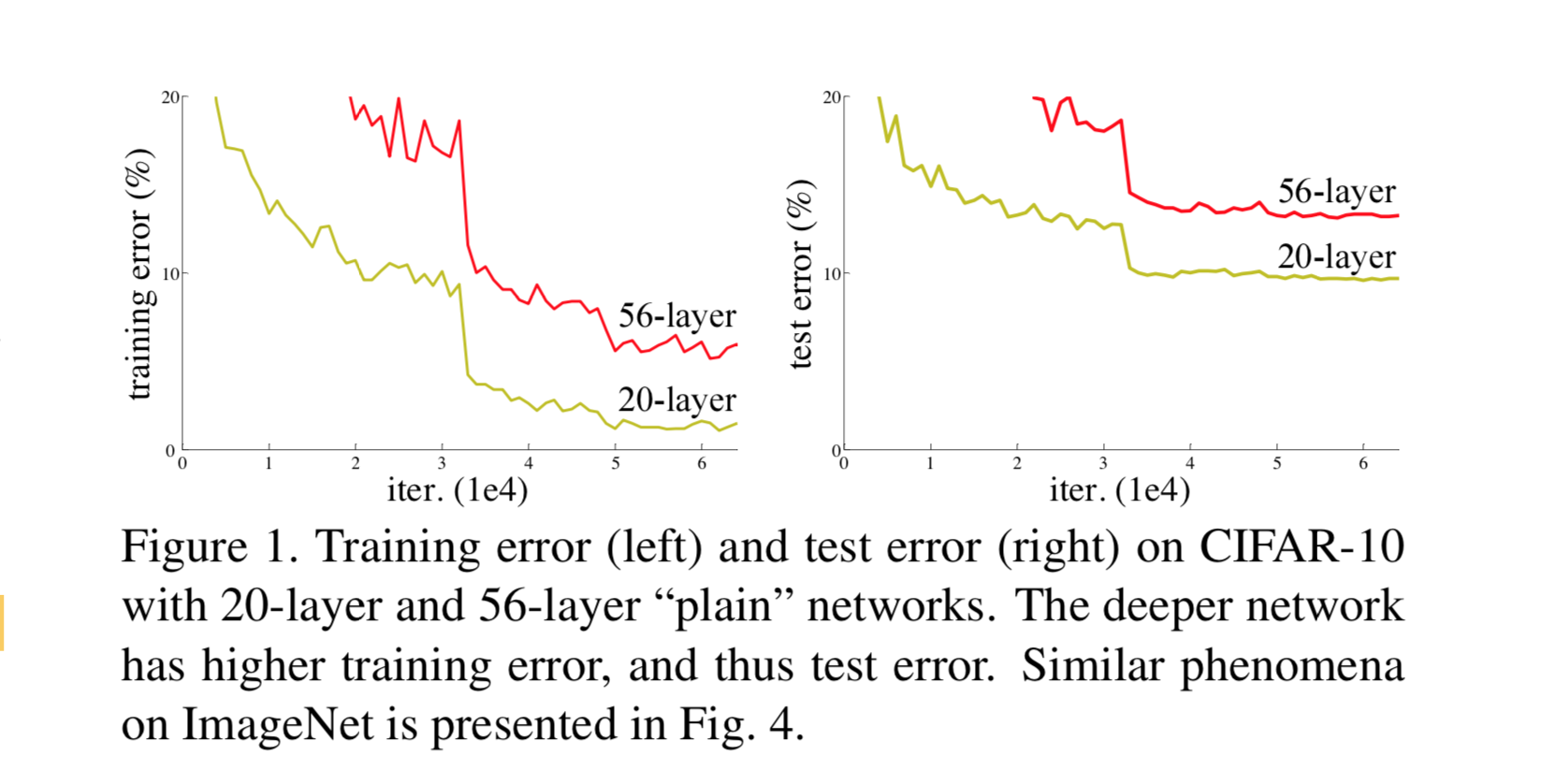
一定程度上缓解梯度破碎问题
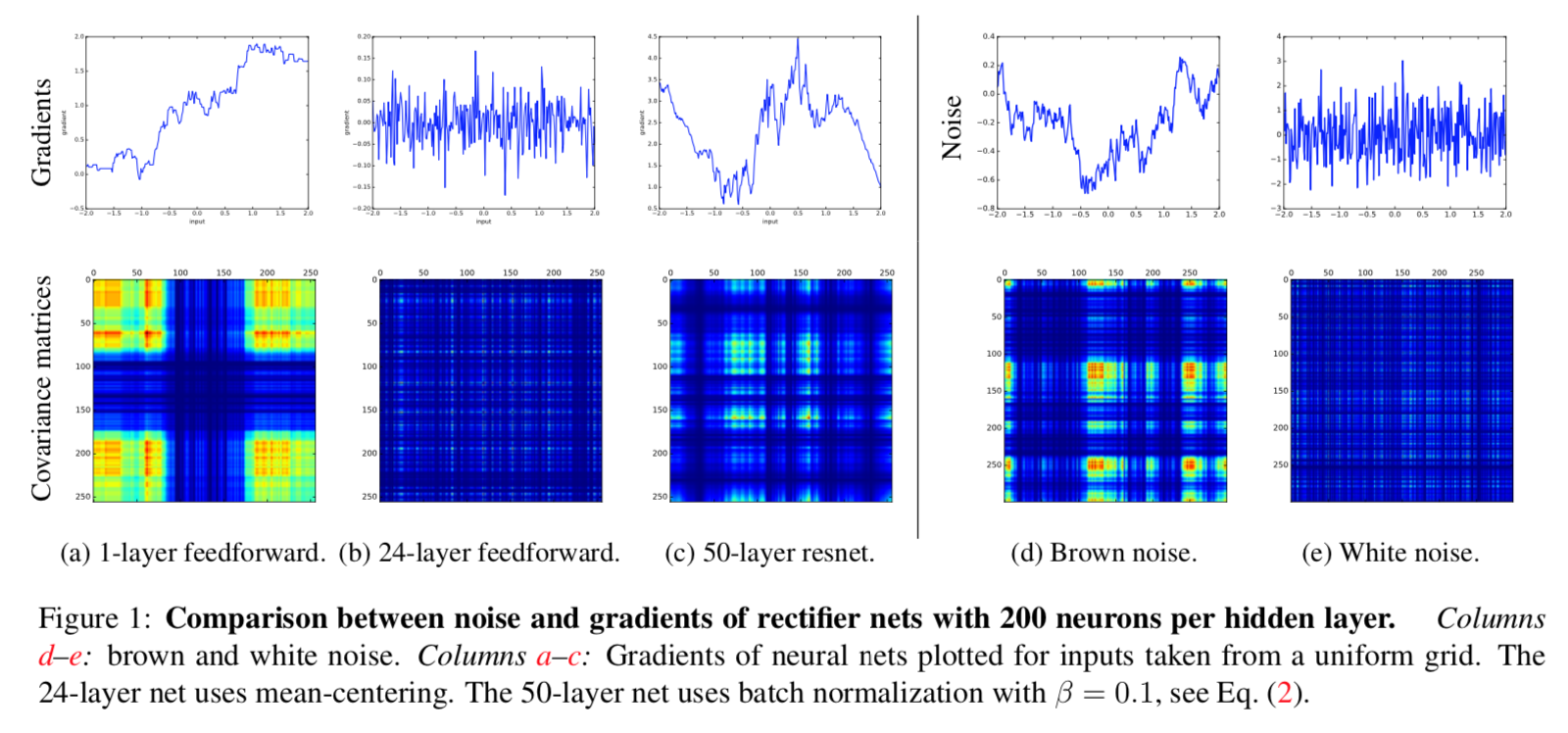
在标准前馈神经网络中,随着深度增加,梯度逐渐呈现为白噪声(white noise)。许多优化方法假设梯度在相邻点上是相似的,破碎的梯度会大大减小这类优化方法的有效性。另外,如果梯度表现得像白噪声,那么某个神经元对网络输出的影响将会很不稳定。
残差模块的结构#
一个残差块(shortcut connections/skip connections)分为直接映射部分\(\left(x_{l}\right)\)和残差部分\(F\left(x_{l}, W_{l}\right)\),可以表示为:
示意图如下图所示:
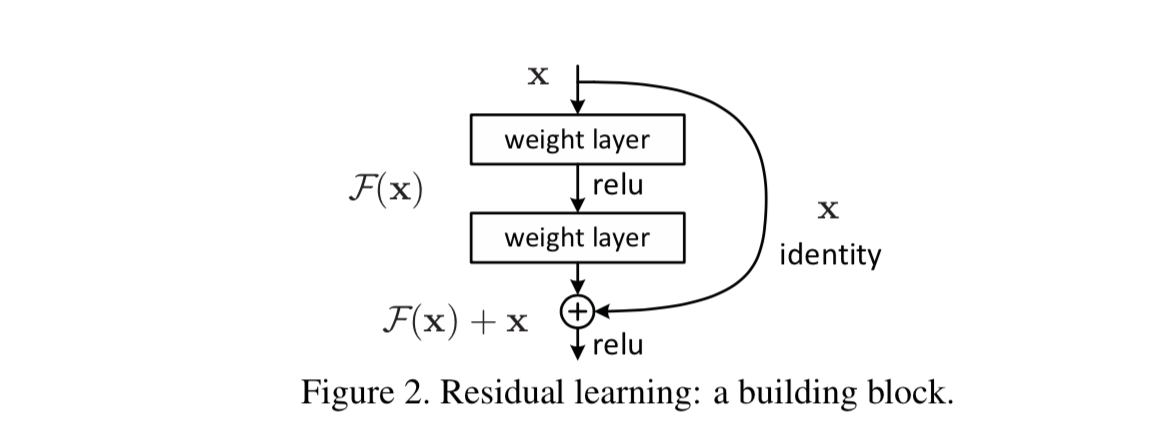
残差模块如何解决上述问题#
根据后向传播的链式法则可以看到,上述残差块中,因为增加了\(x\)项(恒等映射),那么该网络求\(x\)的偏导的时候,多了一项常数1,所以反向传播过程,梯度连乘,也不会造成梯度消失。

在前向传播时,输入信号可以从任意低层直接传播到高层。由于包含了一个天然的恒等映射,一定程度上可以解决网络退化问题。
The Shattered Gradients Problem: If resnets are the answer, then what is the question? 一文中提到在标准前馈神经网络中,随着深度增加,神经元梯度的相关性(corelation)按指数级减少 (\(\frac{1}{2^L}\));同时,梯度的空间结构也随着深度增加被逐渐消除。这也就是梯度破碎现象。