1-Model

1-Model#

在当前人工智能领域, 主流大模型从架构上大致可分为稠密（Dense）模型和混合专家（Mixture of Expert, MoE）模型。稠密模型中所有参数在每次计算时都会参与运算；混合专家模型则将不同的 “专家” 模块组合, 根据输入选择合适的专家处理, 能在保证效果的同时减少计算量和参数量.

MiniMind 系列模型在 Llama 3.1 的基础上设计, 基于经典的 Transformer Deocder-Only 架构，在这一板块, 我们将围绕 MiniMind 系列模型的源代码展开学习.

MiniMind Dense Model#

作者提供了对其 MiniMind Dense Model 模型结构的可视化：

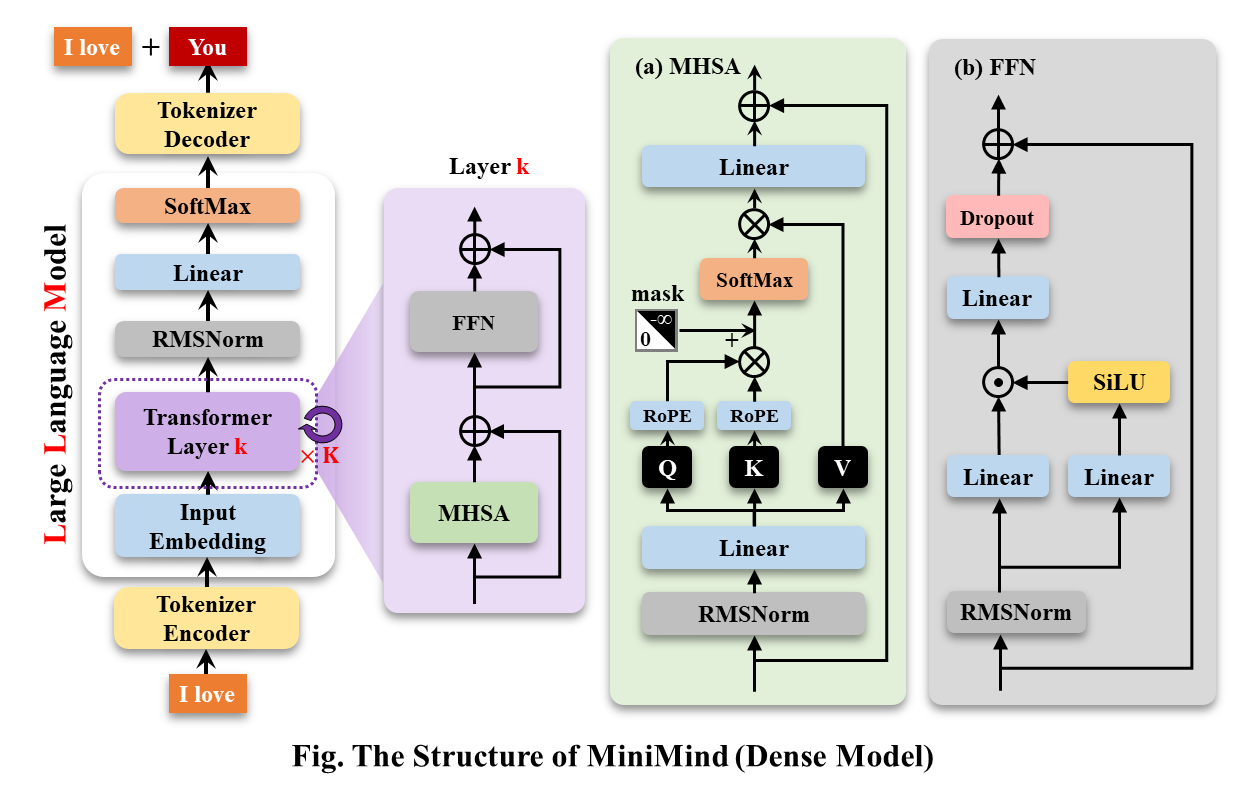
# -------------------- 导入标准库 --------------------
# 导入数学库，用于一些数学运算，比如开方（sqrt）
import math
# 导入struct库，通常用于处理C语言结构体和二进制数据，这里可能用于底层数据操作
import struct
# 导入inspect库，用于获取对象信息，比如函数、类等
import inspect
# 导入时间库，可以用来计算代码运行时间
import time

# -------------------- 导入自定义和第三方库 --------------------
# 从 model 文件夹下的 LMConfig.py 文件中，导入 LMConfig 这个类
# LMConfig 就像一个模型的“配置说明书”，里面定义了模型的所有超参数（比如层数、头数、维度等）
from model.LMConfig import LMConfig
# 从 typing 库导入一些类型提示工具，让代码更清晰易读，告诉我们变量应该是什么类型
# Any: 任何类型
# Optional: 表示一个变量可以是某种类型，也可以是 None (空值)
# Tuple: 元组，一个不可变的列表
# List: 列表
from typing import Any, Optional, Tuple, List
# 导入 NumPy 库，这是Python中科学计算的基础包，常用于处理大型多维数组和矩阵
import numpy as np
# 导入 PyTorch 库，这是我们构建神经网络的核心框架
import torch
# 从 PyTorch 中导入 functional 模块，通常简写为 F。它包含了很多有用的函数，比如激活函数（ReLU, Softmax等）
import torch.nn.functional as F
# 从 PyTorch 中导入 nn 模块，这是构建神经网络层的基本模块
from torch import nn
# 从 Hugging Face 的 transformers 库中导入 PreTrainedModel 类
# 这是一个非常方便的基类，我们自己的模型可以继承它，从而自动获得加载、保存等常用功能
from transformers import PreTrainedModel
# 从 transformers 库中导入一个特定的输出格式类
# CausalLMOutputWithPast 用来规范化“因果语言模型”的输出，它会包含预测结果、过去的键值对(KV Cache)等信息
from transformers.modeling_outputs import CausalLMOutputWithPast

均方根层归一化 (Root Mean Square Layer Normalization, RMSNorm)#

RMSNorm 是对 LayerNorm 的一个改进, 没有做 re-center 操作（移除了均值项）, 可以看作 LayerNorm 在均值为零时的特例, 使用平方根均值归一化降低噪声影响。

Layer Norm

\[y = \frac{x-E(x)}{\sqrt{Var(x) + \epsilon}} * \gamma + \beta\]

假设输入张量形状为 (batch_size, sequence_length, embedding_dim), 层归一化对 embedding_dim 维度进行归一化操作, 其中, \(\epsilon\) 是一个超参数, 用于防止分母为零导致结果上溢, \(\gamma\), \(\beta\) 均为可学习参数。

RMS Norm

\[a_i=\frac{a_i}{RMS(a) + \epsilon} * \gamma, \quad where \quad RMS(a) = \sqrt{\frac{1}{n}\sum^n_{i=1}a^2_i}.\]

假设输入张量形状为 (batch_size, sequence_length, embedding_dim), RMS Norm 对 embedding_dim 维度进行归一化,其中, 其中, \(\epsilon\) 是一个超参数, 用于防止分母为零导致结果上溢, \(\gamma\) 为可学习参数.

不难发现, 当均值为零时, Layer Norm 退化为 RMS Norm. 这是因为 RMS Norm 在 Layer Norm 的基础上舍弃了中心化操作, 仅用缩放进行归一化, 其不改变数据原本的分布, 有利于激活函数输出的稳定.

# 定义一个名为 RMSNorm 的类，它继承自 torch.nn.Module，这是所有 PyTorch 模型层的基础类
class RMSNorm(torch.nn.Module):
    # __init__ 是类的构造函数，当创建 RMSNorm 对象时会自动调用
    # dim: 整数类型，表示输入数据的特征维度大小
    # eps: 浮点数类型，一个非常小的数，用来防止计算时分母为零
    def __init__(self, dim: int, eps: float):
        # 调用父类 torch.nn.Module 的构造函数，这是必须的步骤
        super().__init__()
        # 将传入的 eps 保存为类的属性，方便后面使用
        self.eps = eps
        # 创建一个可学习的参数 self.weight。它是一个向量，长度为 dim
        # nn.Parameter() 会告诉 PyTorch：这个张量是模型的一部分，需要在训练时更新它的值
        # torch.ones(dim) 初始化这个向量，所有元素都为 1
        # 这个 weight 相当于公式中的缩放因子 γ (gamma)
        self.weight = nn.Parameter(torch.ones(dim))

    # forward 函数定义了这一层的前向传播逻辑，也就是具体如何对输入数据 x 进行计算
    # x: 输入的张量(Tensor)，通常形状是 (batch_size, sequence_length, embedding_dim)
    def forward(self, x):
        # 这一行代码实现了 RMSNorm 的核心公式: a_i = (a_i / sqrt(mean(a_i^2) + eps)) * gamma
        
        # 1. x.pow(2): 计算输入 x 中每个元素的平方
        # 2. .mean(-1, keepdim=True): 沿着最后一个维度（特征维度 dim）计算平方后的均值。
        #    keepdim=True 保持了维度的数量，例如 (B, S, D) -> (B, S, 1)，这样方便后续广播计算
        # 3. + self.eps: 加上我们之前定义的极小数 eps，防止开方根时分母为零
        # 4. torch.rsqrt(...): 计算“平方根的倒数”，即 1 / sqrt(...)。这比先算 sqrt 再算倒数效率更高
        # 5. x.float() * ...: 将输入 x（为了计算精度先转为 float 类型）与上面计算出的归一化系数相乘
        # 6. self.weight * ...: 将归一化后的结果与可学习的权重参数 self.weight 相乘，进行缩放
        # 7. .type_as(x): 最后，将计算结果的数据类型转换回和输入 x 一致的类型
        return self.weight * (x.float() * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)).type_as(x)

Rotary Position Embedding, RoPE#

旋转位置编码是一种能将相对位置信息集成到 self-attention 中, 进而提升 transformer 架构性能的位置编码方式, 和绝对位置编码相比, RoPE 具有很好的外推性, 是目前的主流位置编码方式.

外推性的解释, 通俗来说就是训练的时候限制了 512 的上下文长度，那么推理时如果面对超过该长度的文本，LLM 可能无法正确处理.

绝对位置编码

绝对位置编码是早期 Transformer 架构采用的绝对位置编码方案，及那个每个位置映射为固定的向量表示.

\[f_{t:t\in\{q,k,v\}}(\boldsymbol{x}_i,i)=\boldsymbol{W}_{t:t\in\{q,k,v\}}(\boldsymbol{x}_i+\boldsymbol{p}_i)\]

其中编码向量 \(p_i\) 的计算使用如下公式：

\[\boldsymbol{p}_{i,2t}=\sin\left(k/1000^{2t/d}\right), \boldsymbol{p}_{i,2t+1}=\cos\left(k/1000^{2t/d}\right)\]

正如其名，绝对位置编码只考虑了输入序列中的绝对位置关系，对于 token 之间的相对信息则没有纳入考虑.

旋转位置编码

假定 query 和 key 的内积操作可以被函数 g 表示，该函数 g 的输入是词嵌入向量 \(x_m, x_n\) 和它们之间的相对位置 \(m-n\):

\[<f_q(x_m ,m), f_k(x_n, n)>=g(x_m, x_n, m, n)\]

旋转位置编码就是找到一个使上式成立的位置编码方式.

出于认识的目的，我们省略复杂的数学推导，直接看 RoPE 的的结论：

存在这样一个正交矩阵：

\[\begin{split}\boldsymbol{R}_{\Theta,m}^d=\underbrace{\begin{pmatrix}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\end{pmatrix}}_{\boldsymbol{W}_m}\end{split}\]

其中，\(\Theta=\left\{\theta_i=10000^{-2(i-1)/d},i\in[1,2,\ldots,d/2]\right\}\)

我们可以将 query 和 key 的内积操作转换为与原始向量 \(x\) 相关的以下等价形式：

\[ \boldsymbol{q}_m^\mathbf{T}\boldsymbol{k}_n=\left(\boldsymbol{R}_{\Theta,m}^d\boldsymbol{W}_q\boldsymbol{x}_m\right)^\mathbf{T}\left(\boldsymbol{R}_{\Theta,n}^d\boldsymbol{W}_k\boldsymbol{x}_n\right)=\boldsymbol{x}_m^\mathbf{T}\boldsymbol{W}_q\boldsymbol{R}_{\Theta,n-m}^d\boldsymbol{W}_k\boldsymbol{x}_n \]

其中， \(\boldsymbol{R}_{\Theta,n-m}^d=\left(\boldsymbol{R}_{\Theta,m}^d\right)^\mathbf{T}\boldsymbol{R}_{\Theta,n}^d\).

由于 \(\boldsymbol{R}_{\Theta,m}^d\) 的稀疏性，直接使用矩阵乘法会浪费算力，因此代码中采用下述方式实现：

\[\begin{split}\boldsymbol{R}_{\Theta,m}^{d}\boldsymbol{x}=\begin{pmatrix}x_{0}\\x_{1}\\x_{2}\\x_{3}\\\vdots\\x_{d-2}\\x_{d-1}\end{pmatrix}\otimes\begin{pmatrix}\cos m\theta_{0}\\\cos m\theta_{0}\\\cos m\theta_{1}\\\cos m\theta_{1}\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{pmatrix}+\begin{pmatrix}-x_{1}\\x_{0}\\-x_{3}\\x_{2}\\\vdots\\-x_{d-1}\\x_{d-2}\end{pmatrix}\otimes\begin{pmatrix}\sin m\theta_{0}\\\sin m\theta_{0}\\\sin m\theta_{1}\\\sin m\theta_{1}\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{pmatrix} \end{split}\]

# 这个函数用来预先计算旋转位置编码中需要的复数 `cos(mθ) + i*sin(mθ)`
# dim: 词向量的维度
# end: 句子的最大长度
# theta: 一个超参数，用于计算旋转频率
def precompute_pos_cis(dim: int, end: int = int(32 * 1024), theta: float = 1e6):
    """生成旋转矩阵的复数表示"""
    # 1. 计算旋转角度的基础频率 `theta_i`
    # torch.arange(0, dim, 2): 生成 [0, 2, 4, ..., dim-2]
    # [: (dim // 2)]: 取前 dim/2 个元素
    # 这部分完全是按照 RoPE 论文中的公式来计算频率 freqs
    freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    
    # 2. 创建位置索引 `m`，即 [0, 1, 2, ..., end-1]
    t = torch.arange(end, device=freqs.device)
    
    # 3. 计算每个位置 `m` 和每个频率 `theta_i` 的乘积 `m * theta_i`
    # torch.outer(t, freqs) 会计算 t 和 freqs 中每个元素对的乘积，得到一个 (end, dim/2) 的矩阵
    freqs = torch.outer(t, freqs).float()
    
    # 4. 利用欧拉公式 e^(ix) = cos(x) + i*sin(x) 生成复数
    # torch.polar(r, theta) 会生成 r * (cos(theta) + i*sin(theta))
    # 这里 r (模长) 设置为 1 (torch.ones_like(freqs))，角度就是我们刚计算的 freqs
    # 最终 pos_cis 是一个 (end, dim/2) 的复数张量，存储了所有位置的旋转信息
    pos_cis = torch.polar(torch.ones_like(freqs), freqs)
    return pos_cis

# 这个函数将预计算好的旋转信息应用到 Query (xq) 和 Key (xk) 向量上
def apply_rotary_emb(xq, xk, pos_cis):
    """应用 RoPE"""
    # 这是一个辅助函数，用来调整 pos_cis 的形状，使其能够与 xq, xk 进行广播运算
    def unite_shape(pos_cis, x):
        # x 的形状通常是 (batch_size, seq_len, num_heads, head_dim)
        # pos_cis 的形状是 (seq_len, head_dim/2)
        # 这个函数会把 pos_cis 的形状变成 (1, seq_len, 1, head_dim/2)，这样就能和 x 广播相乘了
        ndim = x.ndim
        assert 0 <= 1 < ndim
        assert pos_cis.shape == (x.shape[1], x.shape[-1])
        shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
        return pos_cis.view(*shape)

    # 1. 把 xq 和 xk 向量看作复数。
    # xq 的形状是 (..., head_dim)，我们把它 reshape 成 (..., head_dim/2, 2)
    # 然后用 view_as_complex 把每对 (实部, 虚部) 数字合并成一个复数
    # 比如向量 [a, b, c, d] 会被看作复数向量 [a+ib, c+id]
    xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
    xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
    
    # 调整 pos_cis 的形状以匹配 xq_
    pos_cis = unite_shape(pos_cis, xq_)
    
    # 2. 执行旋转操作。
    # 复数乘法 (a+ib) * (c+id) 在几何上就对应着旋转和缩放。
    # 因为 pos_cis 的模长是 1，所以这里就是纯粹的旋转操作。
    # `xq_ * pos_cis` 就完成了对 xq 的旋转
    rotated_xq = xq_ * pos_cis
    rotated_xk = xk_ * pos_cis
    
    # 3. 把旋转后的复数向量再变回实数向量。
    # view_as_real 会把复数 [a+ib, c+id] 变回实数张量 [[a, b], [c, d]]
    # flatten(3) 会把最后两个维度合并，恢复成原来的 head_dim 形状
    xq_out = torch.view_as_real(rotated_xq).flatten(3)
    xk_out = torch.view_as_real(rotated_xk).flatten(3)
    
    # 返回与输入类型一致的旋转后的 xq 和 xk
    return xq_out.type_as(xq), xk_out.type_as(xk)

我们知道，RoPE 是在 Attention 阶段生成 Query 和 Key 向量后，对这两个向量进行位置编码的.

对于 MiniMindLM，嵌入维度为 512，注意力头数量为 8，故每一个注意力头的维度应该为 512 / 8 = 64.

我们使用固定形状的张量代表 Query 和 Key 向量，对 RoPE 的应用过程进行观察.

# 这是一个演示代码块，用来展示 RoPE 函数的用法和结果
# 1. 创建两个随机张量来模拟 Query(xq) 和 Key(xk) 向量
#    torch.randn 创建的张量符合标准正态分布（均值为0，方差为1）
#    形状 (2, 16, 4, 64) 分别代表：
#    - batch_size = 2: 一批处理2个句子
#    - sequence_length = 16: 每个句子有16个词
#    - num_heads = 4: 注意力机制有4个头
#    - head_dim = 64: 每个头的维度是64
xq, xk = torch.randn((2, 16, 4, 64)), torch.randn((2, 16, 4, 64))

# 2. 调用 precompute_pos_cis 函数来预计算旋转信息
#    - dim=64: 对应每个头的维度 head_dim
#    - end=16: 对应句子的最大长度 sequence_length
#    计算结果 pos_cis 将会是一个 (16, 32) 的复数张量
pos_cis = precompute_pos_cis(64, 16)

# 3. 打印出 pos_cis 的形状和第一个元素，来直观感受一下它的内容
#    - pos_cis.shape: 应该是 torch.Size([16, 32])
#    - pos_cis[0, 0]: 第一个位置(m=0)的第一个旋转角度(θ_0)对应的复数。
#      因为 m=0，所以 m*θ=0，cos(0)+i*sin(0) = 1+0j，所以应该是(1+0j)
print(f'pos_cis 的形状为 {pos_cis.shape}, 其中 [0, 0] 下标元素为 {pos_cis[0, 0]}')

pos_cis 的形状为 torch.Size([16, 32]), 其中 [0, 0] 下标元素为 (1+0j)

# 接上一个代码块，这里我们实际应用刚才生成的旋转信息 pos_cis
# 1. 调用 apply_rotary_emb 函数
#    - 输入是原始的 xq, xk 和计算好的 pos_cis
#    - 输出是经过旋转（即加入了位置信息）的 xq_rope 和 xk_rope
xq_rope, xk_rope = apply_rotary_emb(xq, xk, pos_cis)

# 2. 打印出经过 RoPE 编码后的新 Query 和 Key 的形状
#    RoPE 不会改变向量的整体形状，它只是在内部对向量的值进行了旋转变换
#    所以输出的形状应该和输入的形状完全一样，都是 torch.Size([2, 16, 4, 64])
print(f'经过 RoPE 编码后的 Query 与 Key 的形状为 {xq_rope.shape},  {xk_rope.shape}')

经过 RoPE 编码后的 Query 与 Key 的形状为 torch.Size([2, 16, 4, 64]),  torch.Size([2, 16, 4, 64])

Attention#

注意力机制（Attention Mechanism）是Transformer架构的核心组件，能够有效捕捉长序列内各元素间的依赖关系. 该机制通过计算输入序列中不同位置元素间的注意力得分，对其重要性进行精准建模，使模型在处理信息时能够聚焦于关键部分，从而显著提升对长序列数据的理解与处理能力.

在 MiniMindLM 模型中, Attention Block 包含以下机制和模块:

GQA
KV Cache
SwiGLU

GQA

分组查询注意力 (Group Querey Attention, GQA) 是对多头自注意力机制的扩展, 通过提供计算效率和模型表达能力的灵活权衡, 实现了查询头的分组.

具体来说, GQA 中将 h 个查询头分为 G 组, 每组包含 h / G 个查询头，并共享一个公共的键和值.

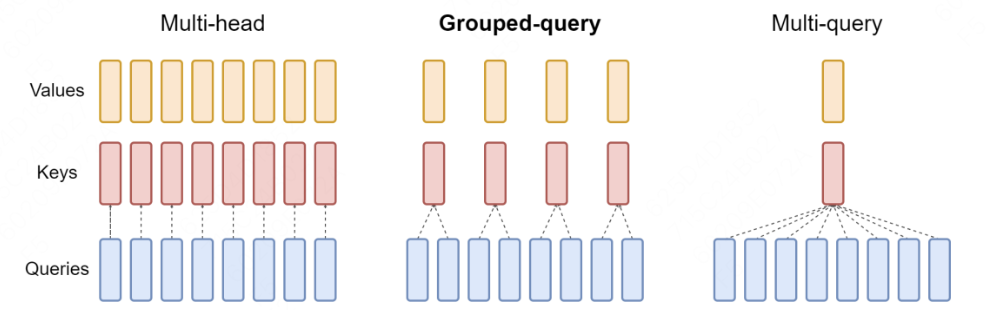
GQA 相比传统的 MHA，减少了键和值的数量，降低了计算量和内存开销，提高了推理速度.

KV Cache

在语言模型生成文本的过程中，每生成一个新的 token，模型都需要计算注意力得分，以确定当前位置与之前所有位置的相关性.

比如以下内容：

seq = [tok1]:

attn_11 = softmax(Q1 * K1.T / sqrt(dim)) * V1
seq = [tok1, tok2]:

attn_11 = softmax(Q1 * K1.T / sqrt(dim)) * V1, attn_12 = 0 (masked)

attn_21 = softmax(Q2 * K1.T / sqrt(dim)) * V1, attn_22 = softmax(Q2 * K2.T / sqrt(dim)) * V2
seq = [tok1, tok2, tok3]:

attn_11 = softmax(Q1 * K1.T / sqrt(dim)) * V1, attn_12 = 0 (masked), attn_13 = 0 (masked)

attn_21 = softmax(Q2 * K1.T / sqrt(dim)) * V1, attn_22 = softmax(Q2 * K2.T / sqrt(dim)) * V2, attn_23 = 0 (masked)

attn_31 = softmax(Q3 * K1.T / sqrt(dim)) * V1, attn_32 = softmax(Q3 * K2.T / sqrt(dim)) * V2, attn_33 = softmax(Q3 * K3.T / sqrt(dim)) * V3
··· ···

不难发现，大模型生成一个 token 后的注意力计算中，总会用到 token 序列的历史 KV 值，导致重复计算，KV Cache 的设计正是为了通过缓存历史 KV 值，节省计算开销.

KV Cache 能够有效压缩大模型推理时的显存占用.

SwiGLU

SwiGLU 是一种在深度学习中用于神经网络架构的激活函数变体：

\[\text{SwiGLU}(x, W, V, b, c)=\text{Swish}_1(xW+b)\otimes(xV+c)\]

与传统的 ReLU 激活函数相比，SwiGLU 具有更好的平滑性和非线性表达能力，由于其门控机制，在处理信息筛选和流动方面有独特的优势.

# 导入一些必要的库
from typing import Any, Optional, Tuple, List
import torch.nn as nn
import math

# 这个函数用于实现分组查询注意力（GQA）中的一个关键步骤
# GQA 中，Key 和 Value 的头数比 Query 的头数少，为了计算注意力，需要把 K 和 V "复制"一下，让它们的头数和 Q 匹配
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
    """使得 KV 头数适应 Query 头数"""
    # 获取输入张量 x 的形状信息
    # bs: batch_size, slen: sequence_length, n_kv_heads: K/V头的数量, head_dim: 每个头的维度
    bs, slen, n_kv_heads, head_dim = x.shape
    # 如果复制次数是1，说明 Q 和 K/V 头数一样（即多头注意力MHA），直接返回即可
    if n_rep == 1:
        return x
    # 否则，进行复制操作
    return (
        # 1. 在第3个维度后增加一个新维度，形状变为 (bs, slen, n_kv_heads, 1, head_dim)
        x[:, :, :, None, :]
        # 2. 使用 expand 在这个新维度上复制 n_rep 次，形状变为 (bs, slen, n_kv_heads, n_rep, head_dim)
        # expand 不会真的复制数据，只是在内存中创建一个视图，非常高效
        .expand(bs, slen, n_kv_heads, n_rep, head_dim)
        # 3. 将 n_kv_heads 和 n_rep 这两个维度合并，最终形状变为 (bs, slen, n_kv_heads * n_rep, head_dim)
        # 这样 K/V 的头数就和 Q 的头数一样了
        .reshape(bs, slen, n_kv_heads * n_rep, head_dim)
    )

# 定义 Attention 类
class Attention(nn.Module):
    # 构造函数，接收一个配置对象 args
    def __init__(self, args: LMConfig):
        super().__init__()
        # K 和 V 的头数。如果没指定，就和 Q 的头数一样
        self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
        # 确保 Q 的头数必须是 K/V 头数的整数倍
        assert args.n_heads % self.n_kv_heads == 0
        # Q 的头数
        self.n_local_heads = args.n_heads
        # K/V 的头数
        self.n_local_kv_heads = args.n_kv_heads
        # 计算复制因子，即每个 K/V 头需要对应多少个 Q 头
        self.n_rep = self.n_local_heads // self.n_local_kv_heads
        # 每个头的维度
        self.head_dim = args.dim // args.n_heads
        
        # 定义四个线性层，用来从输入 x 生成 Q, K, V 和最终的输出
        self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)  # Query 投影
        self.wk = nn.Linear(args.dim, args.n_kv_heads * self.head_dim, bias=False) # Key 投影
        self.wv = nn.Linear(args.dim, args.n_kv_heads * self.head_dim, bias=False) # Value 投影
        self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)    # Output 投影

        # 定义 Dropout 层，用于防止过拟合
        self.attn_dropout = nn.Dropout(args.dropout)
        self.resid_dropout = nn.Dropout(args.dropout)
        self.dropout = args.dropout
        
        # 检查当前 PyTorch 版本是否支持 Flash Attention，并根据配置决定是否使用
        # Flash Attention 是一种高度优化的注意力算法，速度快且省显存
        self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention') and args.flash_attn
        
        # 创建一个上三角矩阵作为“因果遮罩”（causal mask）
        # 这个遮罩的作用是，在预测第 t 个词时，只能看到前 t-1 个词的信息，不能“穿越”到未来
        mask = torch.full((1, 1, args.max_seq_len, args.max_seq_len), float("-inf"))
        mask = torch.triu(mask, diagonal=1)
        # register_buffer 将这个 mask 注册为模型的一部分，但它不是需要训练的参数
        self.register_buffer("mask", mask, persistent=False)

    # 前向传播函数
    def forward(self, 
               x: torch.Tensor,                                      # 输入张量，形状 (bsz, seq_len, dim)
               pos_cis: torch.Tensor,                                # 预计算好的 RoPE 复数
               past_key_value: Optional[Tuple[torch.Tensor, torch.Tensor]] = None, # 上一步的 K/V 缓存
               use_cache=False):                                     # 是否使用 K/V 缓存
        bsz, seq_len, _ = x.shape
        
        # 1. 计算 Q, K, V
        xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
        
        # 2. 将 Q, K, V 的形状调整为多头形式
        xq = xq.view(bsz, seq_len, self.n_local_heads, self.head_dim)
        xk = xk.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)
        xv = xv.view(bsz, seq_len, self.n_local_kv_heads, self.head_dim)
        
        # 3. 应用旋转位置编码 RoPE
        # 注意：RoPE 应该只作用于 Query 和 Key，Value 是不需要位置信息的。
        # 原始代码 `xq, xv = apply_rotary_emb(xq, xk, pos_cis)` 存在笔误，应为 `xq, xk = ...`
        xq, xk = apply_rotary_emb(xq, xk, pos_cis)
        
        # 4. 处理 KV Cache
        # 如果提供了上一步的 K/V (past_key_value)，就把当前的 K/V 和过去的 K/V 拼接起来
        if past_key_value is not None:
            xk = torch.cat([past_key_value[0], xk], dim=1)
            xv = torch.cat([past_key_value[1], xv], dim=1)
            
        # 如果需要使用缓存，就把拼接后的 K/V 保存下来，供下一步使用
        past_kv = (xk, xv) if use_cache else None
        
        # 5. 准备进行注意力计算，交换维度 (seq_len, n_heads) -> (n_heads, seq_len)
        xq = xq.transpose(1, 2)
        xk = repeat_kv(xk, self.n_rep).transpose(1, 2)
        xv = repeat_kv(xv, self.n_rep).transpose(1, 2)
        
        # 6. 计算注意力得分和输出
        if self.flash and seq_len != 1: # 如果使用 Flash Attention (推理时单个token不使用)
            dropout_p = self.dropout if self.training else 0.0
            output = F.scaled_dot_product_attention(xq, xk, xv, attn_mask=None, dropout_p=dropout_p, is_causal=True)
        else: # 如果不使用 Flash Attention，手动计算
            scores = (xq @ xk.transpose(-2, -1)) / math.sqrt(self.head_dim)
            scores += self.mask[:, :, :seq_len, :seq_len] # 加上因果遮罩
            scores = F.softmax(scores.float(), dim=-1).type_as(xq)
            scores = self.attn_dropout(scores)
            output = scores @ xv # 权重 * V
            
        # 7. 最终处理
        output = output.transpose(1, 2).reshape(bsz, seq_len, -1) # 恢复形状
        output = self.resid_dropout(self.wo(output)) # 经过最后的线性层和 Dropout
        
        return output, past_kv

同样的，我们假设一批 batch size = 4， seq len = 16 的 token 序列通过这个 Attention 块，在输入前，它的 input id 会被投影到 dim = 512 维.

# 实例化一个模型配置对象
# LMConfig 是我们预先定义好的一个类，里面包含了模型的所有超参数
# 这里我们创建了一个名为 LMConfig_Dense 的配置实例
# 为了让演示代码跑得快，我们只设置了 n_layers=2，表示这个模型只有2个Transformer Block层。
# 其他未指定的参数（如维度、头数等）将使用 LMConfig 类中定义的默认值。
LMConfig_Dense = LMConfig(n_layers=2)

# 1. 使用刚才创建的配置 `LMConfig_Dense` 来实例化一个 Attention 模块
attn = Attention(LMConfig_Dense)

# 2. 创建一个随机的输入张量 `x` 来模拟一批经过词嵌入后的数据
#    形状 (4, 16, 512) 代表：
#    - batch_size = 4
#    - sequence_length = 16
#    - embedding_dim = 512
x = torch.randn((4, 16, 512))

# 3. 准备 RoPE 旋转信息
#    根据配置，dim=512, n_heads=8, 所以 head_dim = 64
#    句长是 16
pos_cis = precompute_pos_cis(64, 16)

# 4. 将输入 `x` 和 `pos_cis` 送入 Attention 模块进行前向传播
#    - use_cache=True 表示我们希望模块返回计算出的 KV 缓存
#    - `output` 是注意力模块的最终输出
#    - `past_kv` 是一个元组 (key_cache, value_cache)
output, past_kv = attn(x, pos_cis=pos_cis, use_cache=True)

# 5. 打印输入和输出的形状，以验证模块工作是否正常
print(f'输入张量 x ：size = {x.shape}，RoPE 旋转角： size = {pos_cis.shape}')
print(f'输出 output: size = {output.shape},  kv_cache 基本信息：size_key = {past_kv[0].shape}, size_value = {past_kv[1].shape}')

输入张量 x ：size = torch.Size([4, 16, 512])，RoPE 旋转角： size = torch.Size([16, 32])
输出 output: size = torch.Size([4, 16, 512]),  kv_cache 基本信息：size_key = torch.Size([4, 16, 2, 64]), size_value = torch.Size([4, 16, 2, 64])

# `del` 是 Python 的一个关键字，用于删除一个对象
# 这里我们删除 attn 对象，释放它占用的内存（特别是模型参数占用的显存）
# 在 Jupyter Notebook 这种交互式环境中，这是一个好习惯，可以避免不用的变量长时间占用资源
del attn

FeedForward Network#

前馈神经网络接收来自注意力机制层的输出结果，随后对该输出执行进一步的线性变换. 通过这种方式，网络能够深入挖掘并捕获更为复杂、抽象的特征.

# 定义前馈网络类
class FeedForward(nn.Module):
    # 构造函数
    def __init__(self, config: LMConfig):
        super().__init__()
        
        # 计算 FFN 中间层的维度 hidden_dim
        if config.hidden_dim is None:
            # 这是一个经验公式，常见于 Llama 系列模型
            hidden_dim = 4 * config.dim # 1. 通常是输入维度的4倍
            hidden_dim = int(2 * hidden_dim / 3) # 2. 然后取其 2/3
            # 3. 最后向上取整到 multiple_of 的整数倍，这通常是为了硬件（如GPU）计算优化
            #    `(a + b - 1) // b` 是计算 `ceil(a/b)` 的一种整数运算技巧
            config.hidden_dim = config.multiple_of * ((hidden_dim + config.multiple_of - 1) // config.multiple_of)
        
        # 定义三个线性层，这对应 SwiGLU 的结构
        self.w1 = nn.Linear(config.dim, config.hidden_dim, bias=False)
        self.w2 = nn.Linear(config.hidden_dim, config.dim, bias=False)
        self.w3 = nn.Linear(config.dim, config.hidden_dim, bias=False)
        self.dropout = nn.Dropout(config.dropout)

    # 前向传播函数
    def forward(self, x):
        # 这一行实现了 SwiGLU 激活函数: FFN(x) = W2(SiLU(xW1) * xW3)
        # 1. self.w1(x): 第一个线性变换，升维
        # 2. F.silu(...): 应用 SiLU (也叫 Swish) 激活函数
        # 3. self.w3(x): 第三个线性变换，作为“门控”（gate）
        # 4. ... * ...: 将激活后的结果与门控按元素相乘
        # 5. self.w2(...): 进行第二个线性变换，降维，将维度恢复
        # 6. self.dropout(...): 应用 Dropout
        return self.dropout(self.w2(F.silu(self.w1(x)) * self.w3(x)))

设置输入 x 为 batch size = 4，seq len = 16 的 token 序列投影向量，观察 x 在 MiniMind Block 的前向传播过程.

# 1. 使用 `LMConfig_Dense` 配置实例化一个 FeedForward 模块
ffn = FeedForward(LMConfig_Dense)

# 2. 创建一个和之前 Attention 演示中一样的随机输入张量 `x`
x = torch.randn((4, 16, 512))

# 3. 将 `x` 送入 ffn 模块进行前向传播
output = ffn(x)

# 4. 打印输入和输出的形状
#    FFN 模块内部虽然有维度的升降，但其最终输出的维度会和输入维度保持一致
#    所以输入和输出的形状应该是完全相同的
print(f'给定输入 x: size = {x.shape} 下的输出 output：size = {output.shape}')

给定输入 x: size = torch.Size([4, 16, 512]) 下的输出 output：size = torch.Size([4, 16, 512])

# 删除 ffn 对象，释放它占用的内存/显存
del ffn

这就是 Transformer 结构的精妙之处，张量在模型内部进行了各种复杂的投影变形，但是输入输出的张量形状不发生改变!

MiniMind Block#

到目前为止, , 已经完成了 Attention Layer 和 FeedForward Layer 的构建, 所有必须的组件都已经具备, 我们着手构建一个 MiniMind Block

# 定义一个完整的 Transformer Block 类，这是构成大模型的基本单元
class MiniMindBlock(nn.Module):
    # 构造函数
    def __init__(self, layer_id: int, config: LMConfig):
        super().__init__()
        # 保存一些配置信息
        self.n_heads = config.n_heads
        self.dim = config.dim
        self.head_dim = config.dim // config.n_heads
        
        # 实例化一个 Attention 模块
        self.attention = Attention(config)
        self.layer_id = layer_id
        
        # 实例化两个 RMSNorm 层 (这种先归一化再计算的结构称为 Pre-Norm)
        self.attention_norm = RMSNorm(config.dim, eps=config.norm_eps) # 用于 Attention 之前
        self.ffn_norm = RMSNorm(config.dim, eps=config.norm_eps)       # 用于 FeedForward 之前
        
        # 实例化一个 FeedForward 模块
        self.feed_forward = FeedForward(config)

    # 前向传播函数
    def forward(self, x, pos_cis, past_key_value=None, use_cache=False):
        # --- 第一个子层：自注意力 + 残差连接 ---
        # 1. 将 attention 的输出与原始输入 `x` 相加，形成残差连接
        #    这里的 h_attn 是 attention 子层的计算结果
        #    注意 `self.attention_norm(x)`: 输入 `x` 先经过归一化再送入 attention
        h_attn, past_kv = self.attention(self.attention_norm(x), pos_cis, past_key_value=past_key_value, use_cache=use_cache)
        h = x + h_attn
        
        # --- 第二个子层：前馈网络 + 残差连接 ---
        # 1. 将 FFN 的输出与第一个子层的输出 `h` 相加，形成第二个残差连接
        #    注意 `self.ffn_norm(h)`: `h` 先经过归一化再送入 FFN
        out = h + self.feed_forward(self.ffn_norm(h))
        
        # 返回最终的输出和这一层的 KV Cache
        return out, past_kv

我们依然设置输入 x 为 batch size = 4，seq len = 16 的 token 序列投影向量，观察 x 在 MiniMind Block 的前向传播过程.

# 1. 实例化一个 MiniMindBlock
#    - layer_id=1: 假设这是第1层
#    - config=LMConfig_Dense: 使用我们之前创建的配置
miniblock = MiniMindBlock(1, LMConfig_Dense)

# 2. 准备和之前演示一样的输入数据 `x` 和 `pos_cis`
x = torch.randn((4, 16, 512))
pos_cis = precompute_pos_cis(64, 16)

# 3. 将数据送入 miniblock 进行前向传播
out, past_kv = miniblock(x, pos_cis, use_cache=True)

# 4. 打印输出和KV缓存的形状
#    Transformer Block 的一个重要特性是输入和输出的形状保持不变
#    所以 out.shape 应该和 x.shape 一样
print(f'输出 output 信息: size = {out.shape}\n该 Block 维护的 KV Cache 信息：size_key =  {past_kv[0].shape}, size_value = {past_kv[1].shape}')

输出 output 信息: size = torch.Size([4, 16, 512])
该 Block 维护的 KV Cache 信息：size_key =  torch.Size([4, 16, 2, 64]), size_value = torch.Size([4, 16, 2, 64])

# 删除 miniblock 对象，释放内存/显存
del miniblock

MiniMindLM (Dense)#

以 MiniMind Block 为基本组件, 我们对 MiniMindLM 进行最后组装！

from transformers import PreTrainedModel
from transformers.modeling_outputs import CausalLMOutputWithPast

# 定义最终的 MiniMindLM 模型，继承自 PreTrainedModel 以便使用 huggingface 的生态
class MiniMindLM(PreTrainedModel):
    # 指定配置类，huggingface 会用这个来加载和保存配置
    config_class = LMConfig

    def __init__(self, params: LMConfig = None):
        # 如果没有传入配置，就创建一个默认的
        self.params = params or LMConfig()
        super().__init__(self.params)
        self.vocab_size, self.n_layers = params.vocab_size, params.n_layers
        
        # 定义模型的各个组件
        self.tok_embeddings = nn.Embedding(params.vocab_size, params.dim) # 词嵌入层
        self.dropout = nn.Dropout(params.dropout)
        # 使用 nn.ModuleList 创建一个包含 n_layers 个 MiniMindBlock 的列表
        self.layers = nn.ModuleList([MiniMindBlock(l, params) for l in range(self.n_layers)])
        self.norm = RMSNorm(params.dim, eps=params.norm_eps) # 最终的归一化层
        # 输出层：将最终的向量映射回词汇表大小，得到每个词的预测分数 (logits)
        self.output = nn.Linear(params.dim, params.vocab_size, bias=False)
        
        # 权重绑定：让输入嵌入层和输出层的权重共享。这是一个常见的技巧，可以减少参数量并提高性能。
        self.tok_embeddings.weight = self.output.weight
        
        # 预计算并注册 RoPE 的旋转信息
        self.register_buffer("pos_cis", precompute_pos_cis(dim=params.dim // params.n_heads, theta=params.rope_theta), persistent=False)
        # 创建一个标准的输出对象
        self.OUT = CausalLMOutputWithPast()

    # 模型的前向传播逻辑
    def forward(self, input_ids: Optional[torch.Tensor] = None, past_key_values: Optional[List[Tuple[torch.Tensor, torch.Tensor]]] = None, use_cache: bool = False, **args):
        # 初始化 KV 缓存列表
        past_key_values = past_key_values or [None] * len(self.layers)
        start_pos = args.get('start_pos', 0)
        
        # 1. 词嵌入
        h = self.dropout(self.tok_embeddings(input_ids))
        
        # 2. 获取当前序列对应的 RoPE 旋转信息
        pos_cis = self.pos_cis[start_pos: start_pos + input_ids.size(1)]
        
        # 3. 依次通过每一个 Transformer Block
        past_kvs = []
        for l, layer in enumerate(self.layers):
            h, past_kv = layer(h, pos_cis, past_key_value=past_key_values[l], use_cache=use_cache)
            past_kvs.append(past_kv)
            
        # 4. 通过最后的归一化层和输出层，得到 logits
        logits = self.output(self.norm(h))
        
        # 5. 组装并返回标准输出
        self.OUT['logits'] = logits
        self.OUT['aux_loss'] = 0  # 稠密模型没有辅助损失
        self.OUT['past_key_values'] = past_kvs
        return self.OUT

    # 使用 torch.inference_mode() 装饰器，表示这个函数只用于推理，可以进行一些优化
    @torch.inference_mode()
    # 文本生成函数 (高级封装)
    def generate(self, input_ids, eos_token_id=2, max_new_tokens=512, temperature=0.75, top_p=0.90, stream=False, rp=1, use_cache=True, pad_token_id=0, **args):
        if stream: # 如果是流式生成，直接返回生成器
            return self._stream(input_ids, eos_token_id, max_new_tokens, temperature, top_p, rp, use_cache, **args)
        
        # ... (处理 batch, padding 等, 核心是调用 _stream)
        generated = []
        for i in range(input_ids.size(0)):
            non_pad = input_ids[i][input_ids[i] != pad_token_id].unsqueeze(0)
            out = self._stream(non_pad, eos_token_id, max_new_tokens, temperature, top_p, rp, use_cache, **args)
            tokens_list = [tokens for tokens in out] # 收集所有生成的token
            if tokens_list:
                gen = torch.cat(tokens_list, dim=-1)
                full_sequence = torch.cat([non_pad, gen], dim=-1)
            else: # 如果没有生成任何新token
                full_sequence = non_pad
            generated.append(full_sequence)
        
        # ... (将生成的不同长度的序列填充到一样长)
        max_length = max(seq.size(1) for seq in generated)
        padded_generated = [
            F.pad(seq, (0, max_length - seq.size(1)), value=pad_token_id) for seq in generated
        ]
        return torch.cat(padded_generated, dim=0)

    # 核心的逐个 token 生成逻辑
    def _stream(self, input_ids, eos_token_id, max_new_tokens, temperature, top_p, rp, use_cache, **args):
        past_kvs, is_first_step = None, True
        
        for _ in range(max_new_tokens):
            # 1. 模型前向传播
            if is_first_step: # 第一次，处理整个输入序列
                out = self(input_ids, past_key_values=past_kvs, use_cache=use_cache, **args)
                is_first_step = False
            else: # 后续步骤，利用 KV 缓存，只处理最后一个 token
                out = self(input_ids[:, -1:], past_key_values=past_kvs, use_cache=use_cache, start_pos=input_ids.shape[1] - 1, **args)
            
            # 2. 获取预测结果和更新后的 KV 缓存
            logits, past_kvs = out.logits[:, -1, :], out.past_key_values
            
            # 3. 采样：对 logits 进行各种处理
            logits[:, list(set(input_ids.tolist()[0]))] /= rp # 重复惩罚
            logits /= (temperature + 1e-9) # 温度缩放
            if top_p is not None and top_p < 1.0: # Top-p 采样
                # ... (Top-p 采样的标准实现)
                sorted_logits, sorted_indices = torch.sort(logits, descending=True)
                cumulative_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)
                sorted_indices_to_remove = cumulative_probs > top_p
                sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
                sorted_indices_to_remove[..., 0] = 0
                indices_to_remove = sorted_indices_to_remove.scatter(1, sorted_indices, sorted_indices_to_remove)
                logits[indices_to_remove] = -float('Inf')
            
            # 4. 从处理后的 logits 中随机采样一个 token
            probs = F.softmax(logits, dim=-1)
            next_token = torch.multinomial(probs, num_samples=1)
            
            # 5. 将新生成的 token 添加到序列中
            input_ids = torch.cat((input_ids, next_token), dim=1)
            
            # 6. (用于流式输出) yield 当前生成的 token
            yield next_token
            
            # 7. 如果生成了结束符，就停止
            if next_token.item() == eos_token_id:
                break

接下来，我们设置一条长度为 4 的 token 序列，使用 MiniMindLM 对其执行一次前向传播，观察传播过程与返回值.

# 1. 使用 `LMConfig_Dense` 配置实例化一个完整的 MiniMindLM 模型
MiniMind_Dense = MiniMindLM(LMConfig_Dense)

# 2. 创建一个输入序列
#    - torch.Tensor([1, 3, 5, 7]): 包含4个 token ID 的序列
#    - .long(): 将数据类型转为长整型，因为 token ID 必须是整数
#    - .reshape(1, 4): 将其形状变为 (batch_size=1, sequence_length=4)
input_ids = torch.Tensor([1, 3, 5, 7]).long().reshape(1, 4)

# 3. 将输入序列送入模型进行一次完整的前向传播
#    - use_cache=True 表示我们希望模型计算并返回 KV 缓存
OUT = MiniMind_Dense(input_ids, use_cache=True)

# 4. 打印输出结果的各个部分
#    - OUT.logits.shape: 应该是 (1, 4, vocab_size)，表示为序列中每个位置都预测了一个词表大小的概率分布
#    - OUT.aux_loss: 对于稠密模型，这个值是0
#    - len(OUT.past_key_value): 应该等于模型的层数 n_layers，这里是2
print(f'返回 logits：size = {OUT.logits.shape}, 返回 aux_loss: {OUT.aux_loss},  返回 KV Cache List： len = {len(OUT.past_key_value)}')

====> forward propagation started, num_minimind_blocks = 2
------------> entering minimind block: id = 0
<------------ finished, size_cache_k = torch.Size([1, 4, 2, 64]), size_cache_v = torch.Size([1, 4, 2, 64])
------------> entering minimind block: id = 1
<------------ finished, size_cache_k = torch.Size([1, 4, 2, 64]), size_cache_v = torch.Size([1, 4, 2, 64])
<==== forward propagation completed, num_kv_cache = 2

返回 logits：size = torch.Size([1, 4, 6400]), 返回 aux_loss: 0,  返回 KV Cache List： len = 2

# 调用模型的 `generate` 方法来生成文本
# - input_ids: 我们提供的初始文本 [1, 3, 5, 7]
# - max_new_tokens=8: 模型最多会继续生成8个新的 token
# - use_cache=True: 在生成过程中使用 KV 缓存来加速
#   (这意味着只有第一个 token 会处理全部输入，后续 token 都只处理前一个 token)
out = MiniMind_Dense.generate(input_ids, max_new_tokens=8, use_cache=True)

# 打印最终生成的完整序列 (原始输入 + 新生成的部分)
print(f'生成结果：{out}')

gernerating new token: idx = 4
====> forward propagation started, num_minimind_blocks = 2
------------> entering minimind block: id = 0
<------------ finished, size_cache_k = torch.Size([1, 4, 2, 64]), size_cache_v = torch.Size([1, 4, 2, 64])
------------> entering minimind block: id = 1
<------------ finished, size_cache_k = torch.Size([1, 4, 2, 64]), size_cache_v = torch.Size([1, 4, 2, 64])
<==== forward propagation completed, num_kv_cache = 2

gernerating new token: idx = 5
====> forward propagation started, num_minimind_blocks = 2
------------> entering minimind block: id = 0
<------------ finished, size_cache_k = torch.Size([1, 1, 2, 64]), size_cache_v = torch.Size([1, 1, 2, 64])
------------> entering minimind block: id = 1
<------------ finished, size_cache_k = torch.Size([1, 1, 2, 64]), size_cache_v = torch.Size([1, 1, 2, 64])
<==== forward propagation completed, num_kv_cache = 2

gernerating new token: idx = 6
====> forward propagation started, num_minimind_blocks = 2
------------> entering minimind block: id = 0
<------------ finished, size_cache_k = torch.Size([1, 1, 2, 64]), size_cache_v = torch.Size([1, 1, 2, 64])
------------> entering minimind block: id = 1
<------------ finished, size_cache_k = torch.Size([1, 1, 2, 64]), size_cache_v = torch.Size([1, 1, 2, 64])
<==== forward propagation completed, num_kv_cache = 2

new tokens list :[tensor([[2057]]), tensor([[5950]]), tensor([[824]])]

生成结果：tensor([[   1,    3,    5,    7, 2057, 5950,  824]])

# 删除整个 MiniMind_Dense 模型对象，释放其占用的所有资源
del MiniMind_Dense

Minimind MoE Model#

作者提供了 MiniMind MoE Model 的可视化.

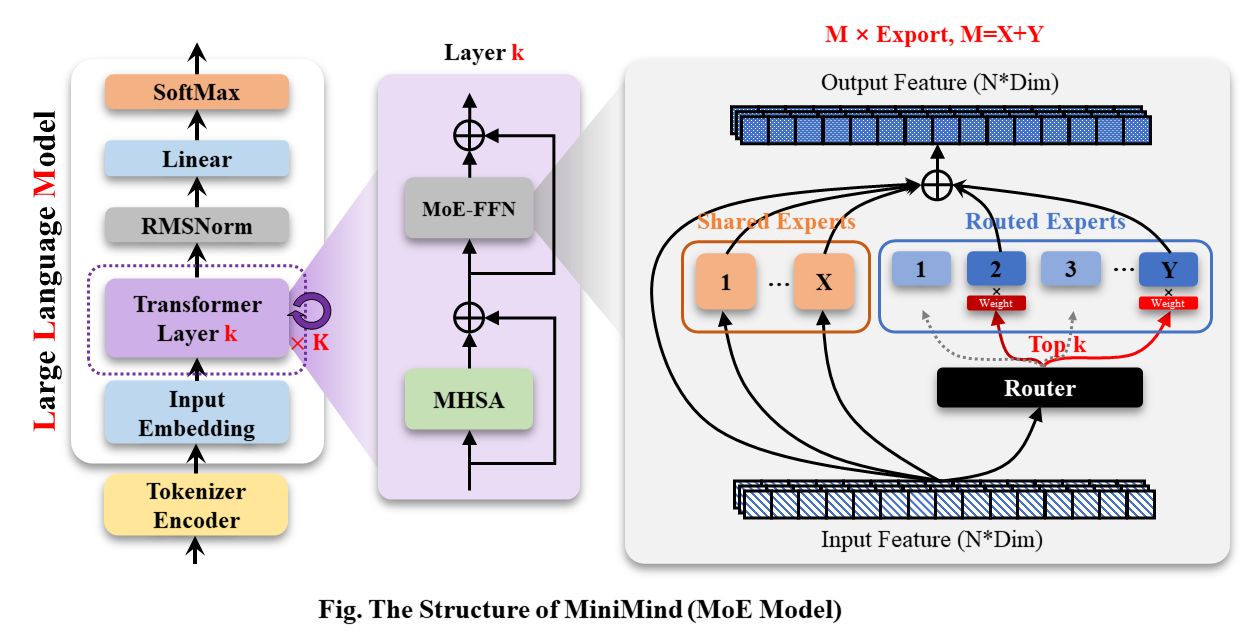
可以看到，Dense Model 和 MoE Model 的差异在于 FFN 层. MoE 模型将稠密连接的 FFN 层置换为 M x Expert 层，每次前向传播时只激活部分 Expert.

其组成可以分为以下部分：

Experts: MoE 架构单元，每个专家本质上是一个独立的神经网络模块，负责处理特定类型或范围的数据.
Router：控制信息流动，决定每次前向传播激活的 Experts 模块以及输入数据在这些模块的分配组合.

在 MoE 网络中，为了平衡专家的重要性，我们需要关注路由，它是决定在特定时间选择哪些专家的重要组件.

辅助损失#

为了让训练过程中实现专家的更均匀分布，辅助损失（又称负载均衡损失）被添加到网络的常规损失中，它增加了一个约束，迫使专家具有相等的重要性.

假设有输入序列 [What is Mixture of Experts], Prob (·) 表示每一个 token 激活的专家概率分布:

Step 1：在整个批次中对每个专家的路由值进行求和.

\[Importance \, per \, token = Prob (What) + Prob (is) + Prob (Mixture) + Prob (of) + Prob (Experts)\]

这个指标反映了 batch 维度上每个专家的重要性分数.
Step 2: 计算变异系数

我们希望专家之间的重要性尽可能靠近，为了衡量专家得分之间的差异程度，引入变异系数指标（Coefficient Variation, CV）

\[Coeifficient \, Variation (CV) = \dfrac{standard \, deviation (\sigma)}{mean(\mu)}\]

如果专家的重要性分数相似，变异系数会降到很低（这是我们期望的）
Step 3: 计算负载均衡损失

\[uxiliary Loss = \alpha * CV\]

其中 \(\alpha\) 是缩放系数.

MoE Gate#

MoE 门控单元决定每次前向传播激活的 Experts 模块及其权重，同时计算 MoE 辅助损失.

# 定义 MoE 的门控网络类，负责为每个token选择专家
class MoEGate(nn.Module):
    def __init__(self, config: LMConfig):
        super().__init__()
        self.config = config
        self.top_k = config.num_experts_per_tok # 每个 token 选择 top_k 个专家
        self.n_routed_experts = config.n_routed_experts # 总专家数量
        self.scoring_func = config.scoring_func
        self.alpha = config.aux_loss_alpha # 负载均衡损失的系数
        self.seq_aux = config.seq_aux
        self.norm_topk_prob = config.norm_topk_prob
        self.gating_dim = config.dim
        # 门控网络的核心参数：一个权重矩阵。
        # 它将输入的 token 向量 (维度 dim) 投影到每个专家的得分上 (维度 n_routed_experts)
        self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
        self.reset_parameter() # 初始化权重

    def reset_parameter(self): # 初始化权重的方法
        import torch.nn.init as init
        init.kaiming_uniform_(self.weight, a=math.sqrt(5)) # 使用 Kaiming 均匀初始化

    def forward(self, hidden_states):
        bsz, seq_len, h = hidden_states.shape
        hidden_states = hidden_states.view(-1, h) # (bsz, seq_len, dim) -> (bsz*seq_len, dim)
        
        # 1. 计算每个 token 对每个专家的原始得分 (logits)
        logits = F.linear(hidden_states, self.weight, None)

        # 2. 将得分转换为概率 (scores)
        if self.scoring_func == 'softmax':
            scores = logits.softmax(dim=-1)
        else:
            raise NotImplementedError(...)

        # 3. 选出得分最高的 top_k 个专家及其权重
        topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)
        
        # 4. (可选) 对 top_k 个专家的权重进行归一化
        if self.top_k > 1 and self.norm_topk_prob:
            topk_weight = topk_weight / (topk_weight.sum(dim=-1, keepdim=True) + 1e-20)

        # 5. (仅在训练时) 计算辅助损失 (auxiliary loss) 以实现负载均衡
        if self.training and self.alpha > 0.0:
            # 这部分是负载均衡损失的数学实现，目标是让所有专家被均匀使用
            # ... (具体实现细节)
            # ...
            pass # 简化，我们知道它在计算一个均衡损失
        else:
            aux_loss = torch.tensor(0.0, device=hidden_states.device)
            
        return topk_idx, topk_

接下来，我们设置一个 batch size = 4, seq len =16, emb dim = 512 的输入向量，在 MoE 门控单元前向传播进行观察

# 创建一个专门用于 MoE 模型的配置
# 与之前的 `LMConfig_Dense` 相比，主要区别在于：
# - `use_moe=True`: 明确告诉模型我们要使用混合专家架构
# 其他参数如 `n_layers=2` 保持不变，以便于和稠密模型对比
LMConfig_MoE = LMConfig(n_layers=2, use_moe=True)

# 1. 使用 MoE 配置实例化一个 MoEGate 模块
gate = MoEGate(LMConfig_MoE)

# 2. 创建一个随机输入张量
#    形状 (4, 16, 512) -> (batch_size, seq_len, dim)
#    总共有 4 * 16 = 64 个 token
hidden_states = torch.randn((4, 16, 512))

# 3. 将输入送入 gate 模块进行前向传播
topk_idx, topk_weight, aux_loss = gate(hidden_states)

# 4. 打印输出结果
#    - topk_idx.shape: 应该是 (64, 2)，因为有64个token，每个选择top_k=2个专家
#    - topk_weight.shape: 同样是 (64, 2)
#    - aux_loss: 负载均衡损失值
print(f'shape: topk_idx = {topk_idx.shape}, topk_weight = {topk_weight.shape}, aux_loss = {aux_loss}')
#    打印第一个 token (token 0) 选择的专家索引和对应的权重
print(f'token 0 选择的专家：idx = {topk_idx[0]}, weight = {topk_weight[0

shape: topk_idx = torch.Size([64, 2]), topk_weight = torch.Size([64, 2]), aux_loss = 0.10178150981664658
token 0 选择的专家：idx = tensor([1, 0]), weight = tensor([3.8736e-21, 3.1941e-21], grad_fn=<SelectBackward0>)
辅助损失：aux_loss = 0.10178150981664658

# 删除 gate 对象，释放内存
del gate

MoE Feed Forward NetWork#

完成 MoE 门控单元的设计后，我们可以对 MoE 前向传播网络进行重新设计.

# 定义 MoE FFN 类
class MoEFeedForward(nn.Module):
    def __init__(self, config: LMConfig):
        super().__init__()
        self.config = config
        # 创建一个专家列表，包含多个独立的 FeedForward 模块
        self.experts = nn.ModuleList([FeedForward(config) for _ in range(config.n_routed_experts)])
        self.gate = MoEGate(config) # 实例化门控网络
        if config.n_shared_experts is not None:
            self.shared_experts = FeedForward(config) # (可选) 共享专家

    def forward(self, x):
        identity = x
        orig_shape = x.shape
        
        # 1. 通过门控网络，获取每个 token 的专家选择和权重
        topk_idx, topk_weight, aux_loss = self.gate(x)
        
        x = x.view(-1, x.shape[-1]) # 拉平输入
        flat_topk_idx = topk_idx.view(-1) # 拉平专家索引
        
        # 2. 根据是训练还是推理，选择不同处理方式
        if self.training:
            # 训练模式：逻辑简单但效率稍低
            x = x.repeat_interleave(self.config.num_experts_per_tok, dim=0)
            y = torch.empty_like(x)
            for i, expert in enumerate(self.experts):
                mask = (flat_topk_idx == i)
                if mask.any():
                    y[mask] = expert(x[mask])
            y = y.view(*topk_weight.shape, -1)
            y = (y * topk_weight.unsqueeze(-1)).sum(dim=1) # 加权求和
            y = y.view(*orig_shape)
        else:
            # 推理模式：调用优化过的 moe_infer 函数
            y = self.moe_infer(x, flat_topk_idx, topk_weight.view(-1, 1)).view(*orig_shape)
            
        if self.config.n_shared_experts is not None:
            y = y + self.shared_experts(identity)
            
        self.aux_loss = aux_loss # 保存辅助损失
        return y

    @torch.no_grad() # 推理时不需要计算梯度
    def moe_infer(self, x, flat_expert_indices, flat_expert_weights):
        # 推理优化：将 token 按专家分组，进行批处理，提高效率
        expert_cache = torch.zeros_like(x)
        idxs = flat_expert_indices.argsort() # 排序，让相同专家的token聚在一起
        tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0) # 计算每个专家的边界
        token_idxs = idxs // self.config.num_experts_per_tok
        for i, end_idx in enumerate(tokens_per_expert):
            start_idx = 0 if i == 0 else tokens_per_expert[i - 1]
            if start_idx == end_idx: continue # 如果没有token分配给这个专家，就跳过
            
            expert = self.experts[i]
            exp_token_idx = token_idxs[start_idx:end_idx]
            expert_tokens = x[exp_token_idx]
            expert_out = expert(expert_tokens).to(expert_cache.dtype) # 专家计算
            expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]]) # 加权
            expert_cache.scatter_add_(0, exp_token_idx.unsqueeze(1).expand_as(expert_out), expert_out) # 将结果放回原位

        return expert_cache