学习率的重要性#
我们继续以一个简单的数学函数作为我们的“山”,来上演一场直观的“下山寻宝”记。
山(损失函数): \(f(x) = x^2 - 6x + 9\)
宝藏(最小值点): \(x=3\)
寻路工具(梯度/导数): \(\frac{dy}{dx}=f'(x) = 2x - 6\)
下山规则(梯度下降): \(x := x - \eta \cdot \frac{dy}{dx}\)
这里的 \(\eta\) (eta) 就是至关重要的学习率。现在,我们从起点 \(x=4\) 出发,看看不同的 \(\eta\) 会带来怎样截然不同的命运。
情况一:没有学习率(或 \(\eta = 1\))—— 永不收敛的震荡#
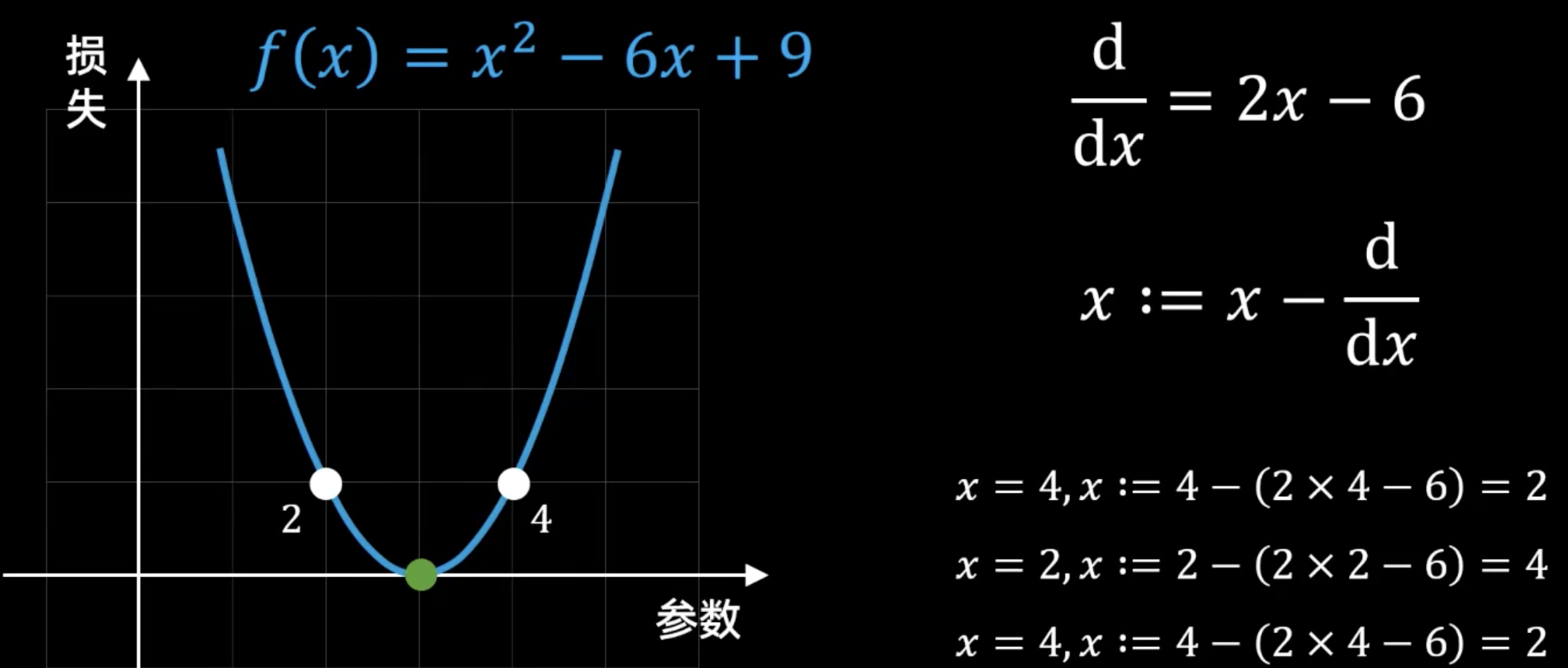
在第一张图中,更新规则写作 \(x := x - \frac{d}{dx}\),这在数学上等价于将学习率 \(\eta\) 设置为 1。这意味着我们完全相信梯度的“建议”,它让我们走多远,我们就走多远。
下山过程:
起始点: \(x = 4\)
计算梯度: \(2x - 6 = 2(4) - 6 = 2\)
更新位置: \(x := 4 - (2) = 2\)
我们从 \(x=4\) 跳到了 \(x=2\),完美地越过了最低点 \(x=3\)。
第二步: 当前位置 \(x = 2\)
计算梯度: \(2x - 6 = 2(2) - 6 = -2\)
更新位置: \(x := 2 - (-2) = 4\)
我们又从 \(x=2\) 跳回了起点 \(x=4\)。
结论(如下图所示):
参数在 2 和 4 之间来回“跳跃”,就像一个乒乓球在山谷两侧来回弹跳,陷入了无限循环的震荡,永远无法稳定在谷底 \(x=3\)。这是因为步子迈得“恰好”能让我们跳到对称的另一边。
情况二:学习率过大(\(\eta = 1.2\))—— 灾难性的发散#
在第二张图中,我们选择了一个更大的学习率 \(\eta = 1.2\)。我们以为步子迈得更大,下山会更快,但结果却适得其反。
下山过程:
起始点: \(x = 4\)
计算梯度: \(2x - 6 = 2(4) - 6 = 2\)
更新位置: \(x := 4 - 1.2 \times (2) = 4 - 2.4 = 1.6\)
我们不仅越过了最低点,而且跳得更远了。
第二步: 当前位置 \(x = 1.6\)
计算梯度: \(2x - 6 = 2(1.6) - 6 = 3.2 - 6 = -2.8\)
更新位置: \(x := 1.6 - 1.2 \times (-2.8) = 1.6 + 3.36 = 4.96\)
这次更新让我们跳回了右侧,但落点 \(4.96\) 比我们的起始点 \(4\) 离谷底更远了!
第三步: 当前位置 \(x = 4.96\)
计算梯度: \(2x - 6 = 2(4.96) - 6 = 3.92\)
更新位置: \(x := 4.96 - 1.2 \times (3.92) = 4.96 - 4.704 = 0.256\)
我们被抛到了一个离谷底更更远的地方。
结论(如下图所示): 参数不仅越过了最低点,而且每一次跳跃都把它带到离最低点越来越远的位置。损失值(山的高度)也随之越来越大。这种情况称为发散 (Divergence)。这就像下山时步子迈得太大,结果一脚踩空,直接滚到了对面的山坡上,而且越滚越高。
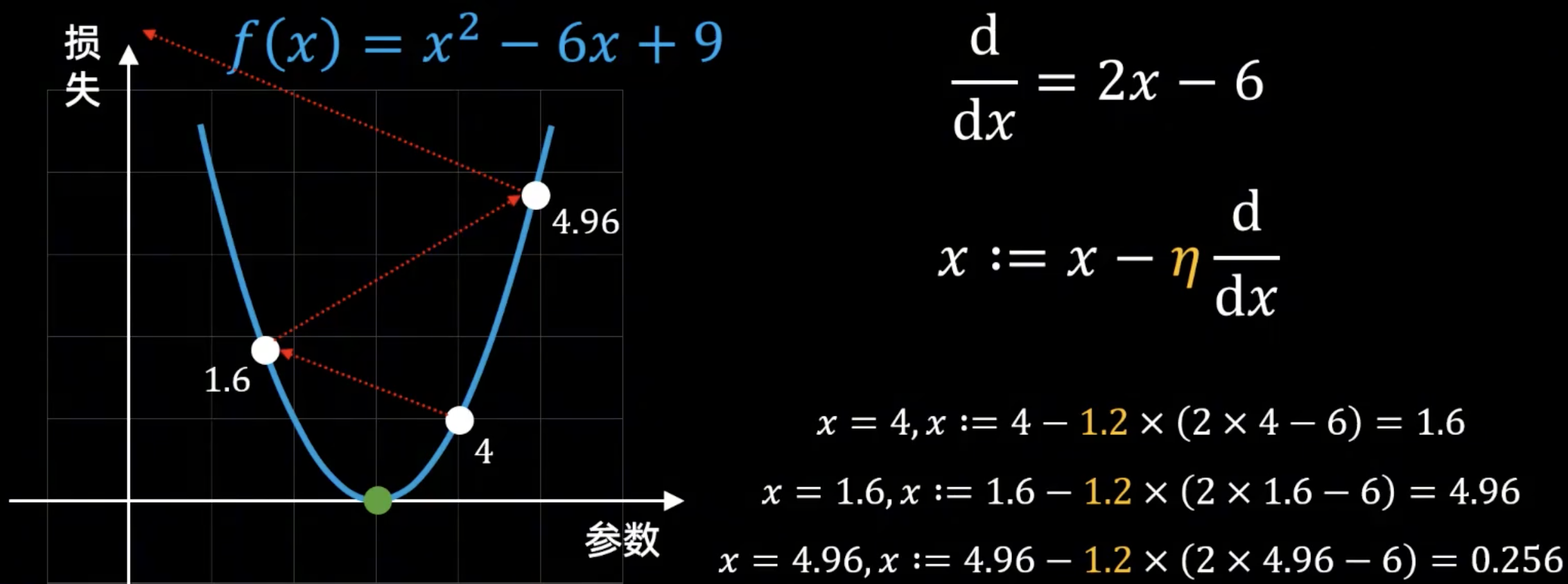
情况三:学习率合适(\(\eta = 0.1\))—— 稳步的收敛#
在第三张图中,我们选择了一个保守但有效的学习率 \(\eta = 0.1\)。我们让每一步都迈得小心翼翼。
下山过程:
起始点: \(x = 4\)
计算梯度: \(2x - 6 = 2(4) - 6 = 2\)
更新位置: \(x := 4 - 0.1 \times (2) = 4 - 0.2 = 3.8\)
我们朝着正确的方向迈出了一小步,离谷底更近了。
第二步: 当前位置 \(x = 3.8\)
计算梯度: \(2x - 6 = 2(3.8) - 6 = 1.6\)
更新位置: \(x := 3.8 - 0.1 \times (1.6) = 3.8 - 0.16 = 3.64\)
又向谷底迈进了一步。
第三步: 当前位置 \(x = 3.64\)
计算梯度: \(2x - 6 = 2(3.64) - 6 = 1.28\)
更新位置: \(x := 3.64 - 0.1 \times (1.28) = 3.64 - 0.128 = 3.512\)
我们稳步前进,无限逼近宝藏所在地 \(x=3\)。
结论(如下图所示): 参数在每一次迭代后,都稳定地向着最低点 \(x=3\) 靠近。步伐不大不小,既保证了方向的正确,又避免了越过最低点。这种情况就是我们最希望看到的收敛 (Convergence)。这就像一位谨慎的登山者,每一步都迈得很稳,确保自己始终在下山,最终安全到达谷底。
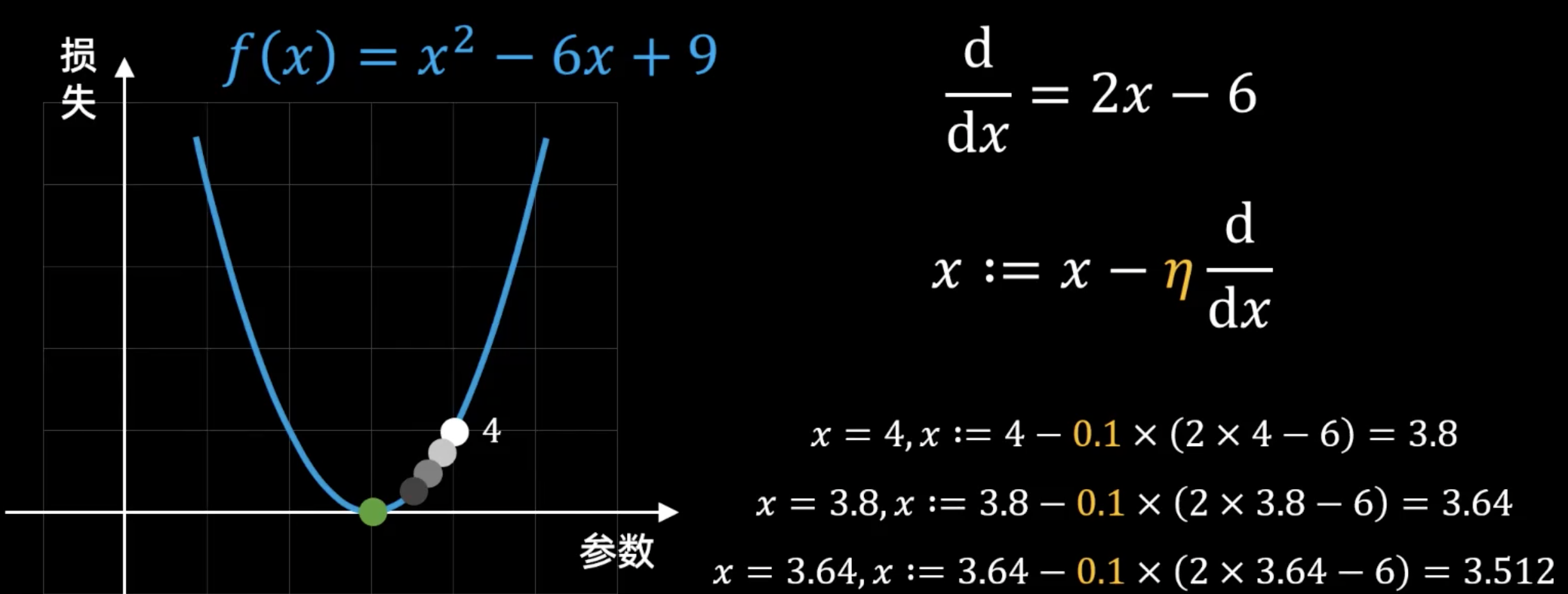
最终总结#
学习率 (\(\eta\)) |
行为 (Behavior) |
结果 (Outcome) |
图像 |
|---|---|---|---|
1.0 |
震荡 (Oscillation) |
无法到达最低点 |
图一 |
1.2 |
发散 (Divergence) |
离最低点越来越远 |
图二 |
0.1 |
收敛 (Convergence) |
稳定地逼近最低点 |
图三 |
这三张图完美地诠释了学习率的真谛:在梯度下降中,梯度告诉我们往哪走(方向),而学习率决定了我们走多远(步长)。选择一个合适的学习率,是在“下山太慢”和“滚下山坡”之间找到最佳平衡的艺术,也是成功训练模型的关键。